One-Dimensional Coulomb Potential

An electron moves in one dimension and is confined to the right half-space (x > 0) where it has a potential energy

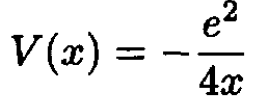(i)

where e is the charge on an electron. This is the image potential of an electron outside a perfect conductor.

a) Find the ground state energy.

b) Find the expectation value ⟨x⟩ in the ground state

SOLUTION

a) Since the electron is confined to the right half-space, its wave function must vanish at the origin. So, an eigenfunction such as exp(-αx) is unsuitable since it does not vanish at x = 0. The ground state wave function must be of the form ѱ = Nx exp(-αa), where α needs to be determined. The operator p² acting on this form gives

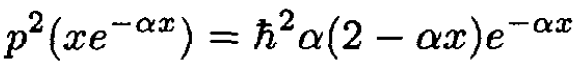(1)

so that using this wave function in Schrodinger’s equation yields

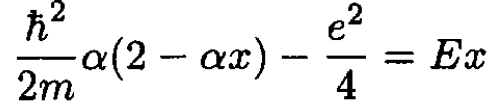(2)

For this equation to be satisfied, the first and third terms on the left must be equal, and the second term on the left must equal the term on the right of the equals sign:

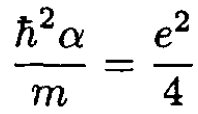(3)

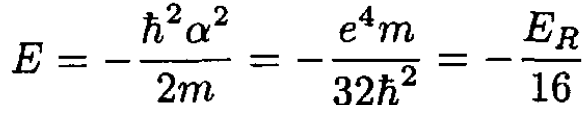(4)

The answer is one sixteenth of the Rydberg, where E_R is the ground state energy of the hydrogen atom. The parameter α = 1/4a₀, where a₀ is the Bohr radius.

b) Next we find the expectation value ⟨x⟩. The first integral is done to find the normalization coefficient:

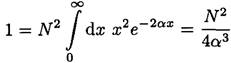(5)

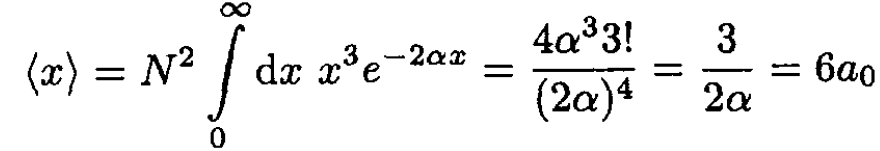(6)

The average value of x is 6 Bohr radii.