المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | علاقة عكسية Inverse Relation |
 2575
 11:28 صباحاً
التاريخ: 20-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 204-205|
أقرأ أيضاً
التاريخ: 4-11-2015
2056
التاريخ: 2-11-2015
1909
التاريخ: 3-11-2015
2029
التاريخ: 3-11-2015
1604
|
إذا كانت ع علاقة ثنائية من المجموعة س إلى المجموعة ص فالعلاقة العكسية ورمزها ع-1 تكون من المجموعة ص إلى المجموعة س بحيث انه لكل نصرين أ ، ب حيث أ∊س,ب∊ص يرتبط العنصر من المجموعة ص بالعنصر من المجموعة س بالعلاقة العكسية ع-1 إذا وفقط إذا كان العنصر من المجموعة س يرتبط بالعنصر من المجموعة ص بالعلاقة ع
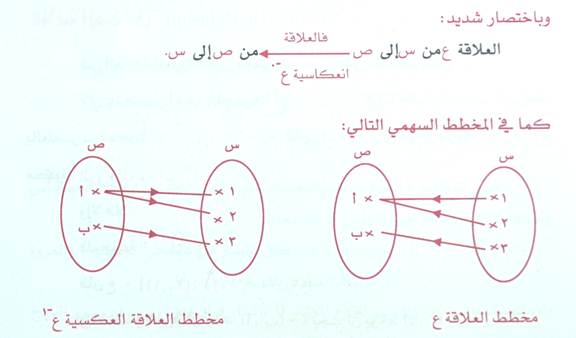
واما بشكل ازواج مرتبة فإننا نبدل المساقط فكان بعضها البعض
فالعلاقة ع = { (1 ، أ) ، ( أ ، 2 ) ، ( ب ، 3)} .
|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|
