The electronic structures of homonuclear diatomic molecules
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
375-377
2025-11-27
44
The electronic structures of homonuclear diatomic molecules
To construct the molecular orbital energy level diagram for Period 2 homonuclear diatomic molecules, we form eight molecular orbitals from the eight valence shell orbitals (four from each atom). In some cases, π orbitals are less strongly bonding than σ orbitals because their maximum overlap occurs off-axis. This relative weakness suggests that the molecular orbital energy level diagram ought to be as shown in Fig. 11.31. However, we must remember that we have assumed that 2s and 2pz orbitals contribute to different sets of molecular orbitals whereas in fact all four atomic orbitals contribute jointly to the four σ orbitals. Hence, there is no guarantee that this order of energies should prevail, and it is found experimentally (by spectroscopy) and by detailed calculation that the order varies along Period 2 (Fig. 11.32). The order shown in Fig. 11.33 is appropriate as far as N2, and Fig. 11.31 applies for O2 and F2. The relative order is controlled by the separation of the 2s and 2p orbitals in the atoms, which increases across the group. The consequent switch in order occurs at about N2. With the orbitals established, we can deduce the ground configurations of the molecules by adding the appropriate number of electrons to the orbitals and following the building-up rules. Anionic species (such as the peroxide ion, O22−) need more electrons than the parent neutral molecules; cationic species (such as O2+) need fewer. Consider N2, which has 10 valence electrons. Two electrons pair, occupy, and fill the 1σg orbital; the next two occupy and fill the 1σu orbital. Six electrons remain. There are two 1πu orbitals, so four electrons can be accommodated in them. The last two enter the 2σg orbital. Therefore, the ground-state configuration of N2 is 1σg2 1σu2 1πu4 2σg2. A measure of the net bonding in a diatomic molecule is its bond order, b:
b = 1/2(n − n*)
where n is the number of electrons in bonding orbitals and n* is the number of electrons in antibonding orbitals. Thus each electron pair in a bonding orbital increases the bond order by 1 and each pair in an antibonding orbital decreases b by 1. For H2, b = 1, corresponding to a single bond, H-H, between the two atoms. In He2, b = 0, and there is no bond. In N2, b = 1/2(8 − 2) = 3. This bond order accords with the Lewis structure of the molecule (:N≡N:).
The ground-state electron configuration of O2, with 12 valence electrons, is based on Fig. 11.31, and is 1σg2 1σu2 2σg2 1πu4 1πg2. Its bond order is 2. According to the building-up principle, however, the two 1πg electrons occupy different orbitals: one will enter 1πu, x and the other will enter 1πu, y. Because the electrons are in different orbitals, they will have parallel spins. Therefore, we can predict that an O2 molecule will have a net spin angular momentum S = 1 and, in the language introduced in Section 10.7, be in a triplet state. Because electron spin is the source of a magnetic moment, we can go on to predict that oxygen should be paramagnetic. This prediction, which VB theory does not make, is confirmed by experiment.
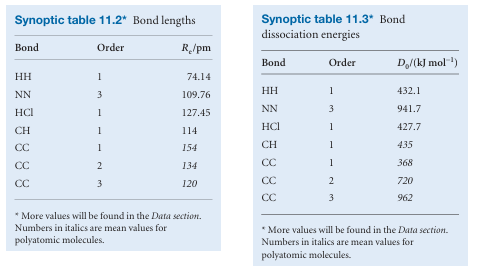
An F2 molecule has two more electrons than an O2molecule. Its configuration is therefore 1σg2 1σu2 2σg2 1πu4 1πg4 and b=1. We conclude that F2 is a singly-bonded molecule, in agreement with its Lewis structure. The hypothetical molecule dineon, Ne2, has two further electrons: its configuration is 1σg 21σu 22σg 21πu 41πg 22σu 2andb=0. The zero-bond order is consistent with the monatomic nature of Ne. The bond order is a useful parameter for discussing the characteristics of bonds, because it correlates with bond length and bond strength. For bonds between atoms of a given pair of elements:
1The greater the bond order, the shorter the bond.
2The greater the bond order, the greater the bond strength. Table 11.2 lists some typical bond lengths in diatomic and polyatomic molecules. The strength of a bond is measured by its bond dissociation energy, De, the energy required to separate the atoms to infinity. Table 11.3 lists some experimental values of dissociation energies.
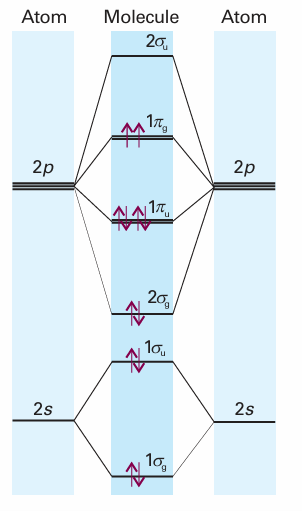
Fig. 11.31 The molecular orbital energy level diagram for homonuclear diatomic molecules. The lines in the middle are an indication of the energies of the molecular orbitals that can be formed by overlap of atomic orbitals. As remarked in the text, this diagram should be used for O2 (the configuration shown) and F2.
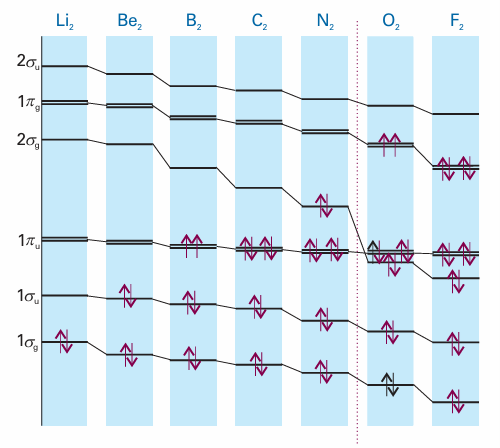
Fig. 11.32 The variation of the orbital energies of Period 2 homonuclear diatomics.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
