
Polyatomic molecules
 المؤلف:
Peter Atkins، Julio de Paula
المؤلف:
Peter Atkins، Julio de Paula
 المصدر:
ATKINS PHYSICAL CHEMISTRY
المصدر:
ATKINS PHYSICAL CHEMISTRY
 الجزء والصفحة:
ص365-367
الجزء والصفحة:
ص365-367
 2025-11-26
2025-11-26
 28
28
Polyatomic molecules
Each σ bond in a polyatomic molecule is formed by the spin pairing of electrons in atomic orbitals with cylindrical symmetry about the relevant internuclear axis. Likewise, π bonds are formed by pairing electrons that occupy atomic orbitals of the appropriate symmetry. The VB description of H2O will make this clear. The valence electron configuration of an O atom is 2s2 2p2x 2p1y 2p1z. The two unpaired electrons in the O2p orbitals can each pair with an electron in an H1s orbital, and each combination results in the formation of a σ bond (each bond has cylindrical symmetry about the respective O-H inter nuclear axis). Because the 2py and 2pz orbitals lie at 90° to each other, the two σ bonds also lie at 90° to each other (Fig. 11.6). We can predict, therefore, that H2O should be an angular molecule, which it is. However, the theory predicts a bond angle of 90°, whereas the actual bond angle is 104.5°.
Another deficiency of VB theory is its inability to account for carbon’s tetravalence (its ability to form four bonds). The ground-state configuration of C is 2s2 2p1x 2p1y, which suggests that a carbon atom should be capable of forming only two bonds, not four. This deficiency is overcome by allowing for promotion, the excitation of an electron to an orbital of higher energy. In carbon, for example, the promotion of a 2s electron to a 2p orbital can be thought of as leading to the configuration
2s2 2p2x 2p1y 2p1z, with four unpaired electrons in separate orbitals. These electrons may pair with four electrons in orbitals provided by four other atoms (such as four H1s orbitals if the molecule is CH4), and hence form four σ bonds. Although energy was required to promote the electron, it is more than recovered by the promoted atom’s ability to form four bonds in place of the two bonds of the unpromoted atom. Promotion, and the formation of four bonds, is a characteristic feature of carbon because the promotion energy is quite small: the promoted electron leaves a doubly occupied 2s orbital and enters a vacant 2p orbital, hence significantly relieving the electron–electron repulsion it experiences in the former. However, we need to remember that promotion is not a ‘real’ process in which an atom somehow becomes excited and then forms bonds: it is a notional contribution to the overall energy change that occurs when bonds form. The description of the bonding in CH4 (and other alkanes) is still incomplete because it implies the presence of three σ bonds of one type (formed from H1s and C2p orbitals) and a fourth σ bond of a distinctly different character (formed from H1s and C2s). This problem is overcome by realizing that the electron density distribution in the promoted atom is equivalent to the electron density in which each electron occupies a hybrid orbital formed by interference between the C2s and C2p orbitals. The origin of the hybridization can be appreciated by thinking of the four atomic orbitals centred on a nucleus as waves that interfere destructively and constructively in different regions, and give rise to four new shapes. The specific linear combinations that give rise to four equivalent hybrid orbitals are
h1 =s+px+py+pz h2 =s−px−py+pz
h3 =s−px+py−pz h4 =s+px−py−pz
As a result of the interference between the component orbitals, each hybrid orbital consists of a large lobe pointing in the direction of one corner of a regular tetrahedron (Fig. 11.7). The angle between the axes of the hybrid orbitals is the tetrahedral angle, 109.47°. Because each hybrid is built from one s orbital and three p orbitals, it is called an sp3hybrid orbital. It is now easy to see how the valence-bond description of the CH4 molecule leads to a tetrahedral molecule containing four equivalent C-H bonds. Each hybrid orbital of the promoted C atom contains a single unpaired electron; an H1s electron can pair with each one, giving rise to a σ bond pointing in a tetrahedral direction. For example, the (un-normalized) wavefunction for the bond formed by the hybrid orbital h1 and the 1sA orbital (with wavefunction that we shall denote A) is
ψ=h1(1)A(2) +h1(2)A(1)
Because each sp3 hybrid orbital has the same composition, all four σ bonds are identical apart from their orientation in space (Fig. 11.8). A hybrid orbital has enhanced amplitude in the internuclear region, which arises from the constructive interference between the s orbital and the positive lobes of the p orbitals (Fig. 11.9). As a result, the bond strength is greater than for a bond formed
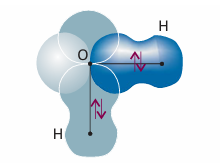
Fig. 11.6 A first approximation to the valence-bond description of bonding in an H2O molecule. Each σ bond arises from the overlap of an H1s orbital with one of the O2porbitals. This model suggests that the bond angle should be 90°, which is significantly different from the experimental value.
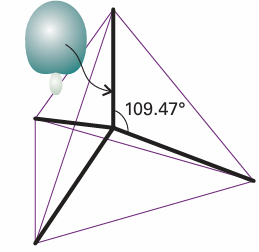
Fig. 11.7 An sp3 hybrid orbital formed from the superposition of s and p orbitals on the same atom. There are four such hybrids: each one points towards the corner of a regular tetrahedron. The overall electron density remains spherically symmetrical.
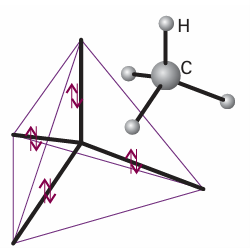
Fig. 11.8 Each sp3 hybrid orbital forms a σ bond by overlap with an H1s orbital located at the corner of the tetrahedron. This model accounts for the equivalence of the four bonds in CH4.
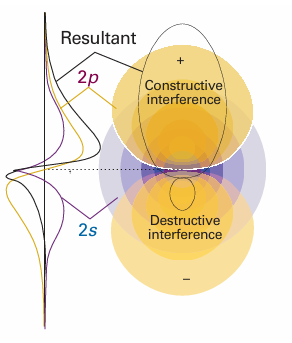
Fig. 11.9 A more detailed representation of the formation of an sp3 hybrid by interference between wavefunctions centred on the same atomic nucleus. (To simplify the representation, we have ignored the radial node of the 2s orbital.)
from an s or p orbital alone. This increased bond strength is another factor that helps to repay the promotion energy. Hybridization can also be used to describe the structure of an ethene molecule, H2C=CH2, and the torsional rigidity of double bonds. An ethene molecule is planar, with HCH and HCC bond angles close to 120°. To reproduce the σ bonding structure, we promote each C atom to a 2s1 2p3 configuration. However, instead of using all four orbitals to form hybrids, we form sp2 hybrid orbitals:
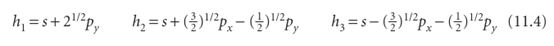
that lie in a plane and point towards the corners of an equilateral triangle (Fig. 11.10). The third 2p orbital (2pz) is not included in the hybridization; its axis is perpendicu lar to the plane in which the hybrids lie. As always in superpositions, the proportion of each orbital in the mixture is given by the square of the corresponding coefficient. Thus, in the first of these hybrids the ratio of s to p contributions is 1:2. Similarly, the total p contribution in each of h2 and h3 is 3/2 + 1/2 = 2, so the ratio for these orbitals is also 1:2. The different signs of the coefficients ensure that constructive interference takes place in different regions of space, so giving the patterns in the illustration. We can now describe the structure of CH2=CH2 as follows. The sp2-hybridized C atoms each form three σ bonds by spin pairing with either the h1 hybrid of the other C atom or with H1s orbitals. The σ framework therefore consists of C-H and C-C σ bonds at 120° to each other. When the two CH2 groups lie in the same plane, the two electrons in the unhybridized p orbitals can pair and form a π bond (Fig. 11.11). The formation of this π bond locks the framework into the planar arrangement, for any rotation of one CH2 group relative to the other leads to a weakening of the π bond (and consequently an increase in energy of the molecule). A similar description applies to ethyne, HC.CH, a linear molecule. Now the C atoms are sp hybridized, and the σ bonds are formed using hybrid atomic orbitals of the form
h1 =s+pz h2 =s−pz
These two orbitals lie along the internuclear axis. The electrons in them pair either with an electron in the corresponding hybrid orbital on the other C atom or with an electron in one of the H1s orbitals. Electrons in the two remaining p orbitals on each atom, which are perpendicular to the molecular axis, pair to form two perpendicular πbonds (Fig. 11.12).
Other hybridization schemes, particularly those involving d orbitals, are often invoked in elementary work to be consistent with other molecular geometries (Table 11.1). The hybridization of N atomic orbitals always results in the formation of Nhybrid orbitals, which may either form bonds or may contain lone pairs of electrons. For example, sp3d2 hybridization results in six equivalent hybrid orbitals pointing towards the corners of a regular octahedron and is sometimes invoked to account for the structure of octahedral molecules, such as SF6.
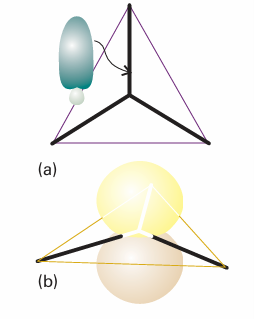
Fig. 11.10 (a) An s orbital and two p orbitals can be hybridized to form three equivalent orbitals that point towards the corners of an equilateral triangle. (b) The remaining, unhybridized p orbital is perpendicular to the plane.
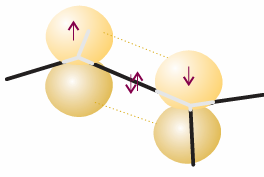
Fig. 11.11 A representation of the structure of a double bond in ethene; only the π bond is shown explicitly.
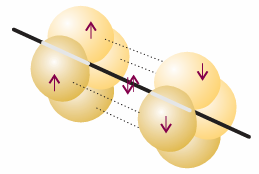
Fig. 11.12 A representation of the structure of a triple bond in ethyne; only the π bonds are shown explicitly. The overall electron density has cylindrical symmetry around the axis of the molecule.
 الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


