Singlet and triplet states
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص347-348
2025-11-26
22
Singlet and triplet states
Suppose we were interested in the energy levels of a He atom, with its two electrons. We know that the ground-state configuration is 1s2, and can anticipate that an excited configuration will be one in which one of the electrons has been promoted into a 2s orbital, giving the configuration 1s1 2s1. The two electrons need not be paired because they occupy different orbitals. According to Hund’s maximum multiplicity rule, the state of the atom with the spins parallel lies lower in energy than the state in which they are paired. Both states are permissible, and can contribute to the spectrum of the atom. Parallel and antiparallel (paired) spins differ in their overall spin angular momentum. In the paired case, the two spin momenta cancel each other, and there is zero net spin (as was depicted in Fig. 10.18). The paired-spin arrangement is called a singlet. Its spin state is the one we denoted σ− in the discussion of the Pauli principle: σ−(1,2) = (1/2 1/2){α(1)β(2) − β(1)α(2)}.
The angular momenta of two parallel spins add together to give a nonzero total spin, and the resulting state is called a triplet. As illustrated in Fig. 10.24, there are three ways of achieving a nonzero total spin, but only one way to achieve zero spin. The three spin states are the symmetric combinations introduced earlier: α(1)α(2) σ+(1,2) = (1/2 1/2){α(1)β(2) + β(1)α(2)} β(1)β(2) .
The fact that the parallel arrangement of spins in the 1s12s1 configuration of the He atom lies lower in energy than the antiparallel arrangement can now be expressed by saying that the triplet state of the 1s1 2s1 configuration of He lies lower in energy than the singlet state. This is a general conclusion that applies to other atoms (and molecules) and, for states arising from the same configuration, the triplet state generally lies lower than the singlet state. The origin of the energy difference lies in the effect of spin correlation on the Coulombic interactions between electrons, as we saw in the case of Hund’s rule for ground-state configurations. Because the Coulombic inter action between electrons in an atom is strong, the difference in energies between singlet and triplet states of the same configuration can be large. The two states of 1s1 2s1 He, for instance, differ by 6421 cm−1 (corresponding to 0.80 eV).
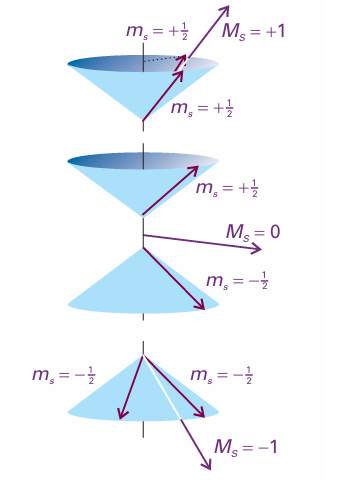
Fig. 10.24 When two electrons have parallel spins, they have a nonzero total spin angular momentum. There are three ways of achieving this resultant, which are shown by these vector representations. Note that, although we cannot know the orientation of the spin vectors on the cones, the angle between the vectors is the same in all three cases, for all three arrangements have the same total spin angular momentum (that is, the resultant of the two vectors has the same length in each case, but points in different directions). Compare this diagram with Fig. 10.18, which shows the antiparallel case. Note that, whereas two paired spins are precisely antiparallel, two ‘parallel’ spins are not strictly parallel.
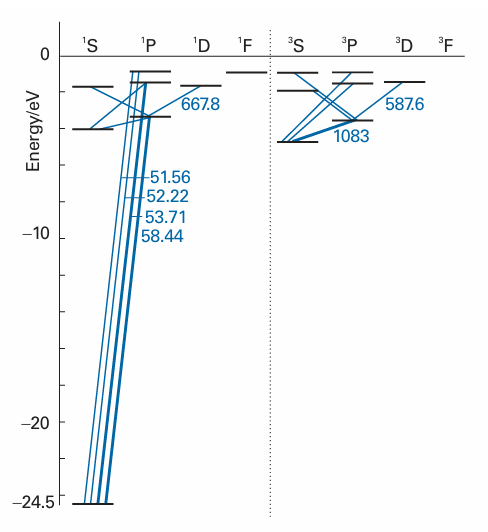
Fig. 10.25 Part of the Grotrian diagram for a helium atom. Note that there are no transitions between the singlet and triplet levels.
The spectrum of atomic helium is more complicated than that of atomic hydrogen, but there are two simplifying features. One is that the only excited configurations it is necessary to consider are of the form 1s1nl1: that is, only one electron is excited. Excitation of two electrons requires an energy greater than the ionization energy of the atom, so the He+ ion is formed instead of the doubly excited atom. Second, no radiative transitions take place between singlet and triplet states because the relative orientation of the two electron spins cannot change during a transition. Thus, there is a spectrum arising from transitions between singlet states (including the ground state) and between triplet states, but not between the two. Spectroscopically, helium behaves like two distinct species, and the early spectroscopists actually thought of helium as consisting of ‘parahelium’ and ‘orthohelium’. The Grotrian diagram for helium in Fig. 10.25 shows the two sets of transitions.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
