Homonuclear diatomic molecules
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص363-365
2025-11-26
25
Homonuclear diatomic molecules
In VB theory, a bond is regarded as forming when an electron in an atomic orbital on one atom pairs its spin with that of an electron in an atomic orbital on another atom. To understand why this pairing leads to bonding, we have to examine the wavefunction for the two electrons that form the bond. We begin by considering the simplest possible chemical bond, the one in molecular hydrogen, H2. The spatial wavefunction for an electron on each of two widely separated H atoms is ψ=χH1sA (r1) χH1sB (r2) if electron 1 is on atom A and electron 2 is on atom B; in this chapter we use χ (chi) to denote atomic orbitals. For simplicity, we shall write this wavefunction as ψ = A (1)B(2). When the atoms are close, it is not possible to know whether it is electron 1 that is on A or electron 2. An equally valid description is therefore ψ = A (2)B(1), in which electron 2 is on A and electron 1 is on B. When two outcomes are equally probable, quantum mechanics instructs us to describe the true state of the system as a super position of the wavefunctions for each possibility (Section 8.5d), so a better description of the molecule than either wavefunction alone is the (unnormalized) linear combination
ψ=A (1)B(2) ±A (2)B(1)
It turns out that the combination with lower energy is the one with a + sign, so the valence-bond wavefunction of the H2 molecule is
ψ=A (1)B(2) +A(2)B(1)
The formation of the bond in H2 can be pictured as due to the high probability that the two electrons will be found between the two nuclei and hence will bind them together. More formally, the wave pattern represented by the term A(1)B(2) interferes constructively with the wave pattern represented by the contribution A(2)B(1), and there is an enhancement in the value of the wavefunction in the internuclear region (Fig. 11.2).
The electron distribution described by the wavefunction in eqn 11.2 is called a σ bond. A σ bond has cylindrical symmetry around the internuclear axis, and is so called because, when viewed along the internuclear axis, it resembles a pair of electrons in an s orbital (and σ is the Greek equivalent of s). A chemist’s picture of a covalent bond is one in which the spins of two electrons pair as the atomic orbitals overlap. The origin of the role of spin is that the wavefunction given in eqn 11.2 can be formed only by a pair of electrons with opposed spins. Spin pairing is not an end in itself: it is a means of achieving a wavefunction (and the probability distribution it implies) that corresponds to a low energy.
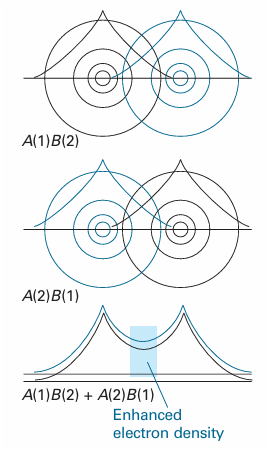
Fig. 11.2 It is very difficult to represent valence-bond wavefunctions because they refer to two electrons simultaneously. However, this illustration is an attempt. The atomic orbital for electron 1 is represented by the black contours, and that of electron 2 is represented by the blue contours. The top illustration represents A(1)B(2), and the middle illustration represents the contribution A(2)B(1). When the two contributions are superimposed, there is interference between the black contributions and between the blue contributions, resulting in an enhanced (two-electron) density in the internuclear region.
Justification 11.1 Electron pairing in VB theory The Pauli principle requires the wavefunction of two electrons to change sign when the labels of the electrons are interchanged (see Section 10.4b). The total VB wave function for two electrons is
ψ(1,2) = {A(1)B(2) + A(2)B(1)}σ(1,2)
where σ represents the spin component of the wavefunction. When the labels 1 and 2 are interchanged, this wavefunction becomes
ψ(2,1) = {A(2)B(1) + A(1)B(2)}σ(2,1) = {A(1)B(2) + A(2)B(1)}σ(2,1) The Pauli principle requires that ψ(2,1) =−ψ(1,2), which is satisfied only if σ(2,1) =−σ(1,2). The combination of two spins that has this property is
σ−(1,2) = (1/21/2){α(1)β(2) − α(2)β(1)}
which corresponds to paired electron spins (Section 10.7). Therefore, we conclude that the state of lower energy (and hence the formation of a chemical bond) is achieved if the electron spins are paired.
The VB description of H2 can be applied to other homonuclear diatomic molecules, such as nitrogen, N2. To construct the valence bond description of N2, we consider the valence electron configuration of each atom, which is 2s22px 12py 12pz 1. It is conventional to take the z-axis to be the internuclear axis, so we can imagine each atom as having a 2pz orbital pointing towards a 2pz orbital on the other atom (Fig. 11.3), with the 2px and 2py orbitals perpendicular to the axis. A σ bond is then formed by spin pairing between the two electrons in the two 2pz orbitals. Its spatial wavefunction is given by eqn 11.2, but now A and B stand for the two 2pz orbitals.
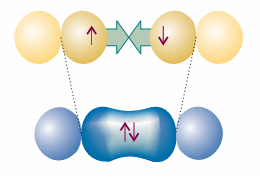
Fig. 11.3 The orbital overlap and spin pairing between electrons in two collinear p orbitals that results in the formation of a σ bond.
The remaining 2p orbitals cannot merge to give σ bonds as they do not have cylindrical symmetry around the internuclear axis. Instead, they merge to form two π bonds. A π bond arises from the spin pairing of electrons in two p orbitals that approach side-by-side (Fig. 11.4). It is so called because, viewed along the inter nuclear axis, a π bond resembles a pair of electrons in a p orbital (and π is the Greek equivalent of p). There are two π bonds in N2, one formed by spin pairing in two neighbouring 2px orbitals and the other by spin pairing in two neighbouring 2py orbitals. The overall bonding pattern in N2is therefore a σ bond plus two πbonds (Fig. 11.5), which is consistent with the Lewis structure: N.N: for nitrogen.
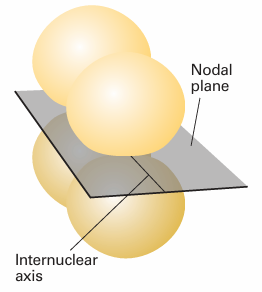
Fig. 11.4 A π bond results from orbital overlap and spin pairing between electrons in p orbitals with their axes perpendicular to the internuclear axis. The bond has two lobes of electron density separated by a nodal plane.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
