Linear combinations of atomic orbitals
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص369-370
2025-11-26
30
Linear combinations of atomic orbitals
If an electron can be found in an atomic orbital belonging to atom A and also in an atomic orbital belonging to atom B, then the overall wavefunction is a superposition of the two atomic orbitals:
ψ±=N(A±B)
where, for H2+, A denotes χH1sA , B denotes χH1sB , and N is a normalization factor. The technical term for the superposition in eqn 11.7 is a linear combination of atomic orbitals (LCAO). An approximate molecular orbital formed from a linear combination of atomic orbitals is called an LCAO-MO. A molecular orbital that has cylindrical symmetry around the internuclear axis, such as the one we are discussing, is called a σ orbital because it resembles an s orbital when viewed along the axis and, more precisely, because it has zero orbital angular momentum around the internuclear axis.
Fig. 11.13 (a) The amplitude of the bonding molecular orbital in a hydrogen molecule ion in a plane containing the two nuclei and (b) a contour representation of the amplitude.
Figure 11.13 shows the contours of constant amplitude for the two molecular orbitals in eqn 11.7, and Fig. 11.14 shows their boundary surfaces. Plots like these are readily obtained using commercially available software. The calculation is quite straightforward, because all we need do is feed in the mathematical forms of the two atomic orbitals and then let the program do the rest. In this case, we use
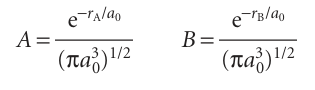
and note that rA and rB are not independent (2), but related by the law of cosines (see Comment 11.3):
rB = {rA2 + R2 − 2rAR cos θ}1/2
To make this plot, we have taken N2 = 0.31 (Example 11.1).
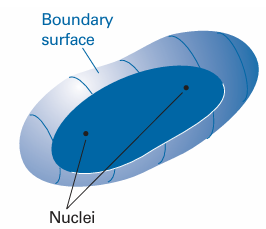
Fig. 11.14 A general indication of the shape of the boundary surface of a σ orbital.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
