


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-04-19
التاريخ: 2023-04-20
التاريخ: 2023-04-26
التاريخ: 2023-04-17
|
Are all the laws of physics reversible? Evidently not! Just try to unscramble an egg! Run a moving picture backwards, and it takes only a few minutes for everybody to start laughing. The most natural characteristic of all phenomena is their obvious irreversibility.
Where does irreversibility come from? It does not come from Newton’s laws. If we claim that the behavior of everything is ultimately to be understood in terms of the laws of physics, and if it also turns out that all the equations have the fantastic property that if we put t=−t we have another solution, then every phenomenon is reversible. How then does it come about in nature on a large scale that things are not reversible? Obviously there must be some law, some obscure but fundamental equation, perhaps in electricity, maybe in neutrino physics, in which it does matter which way time goes.
Let us discuss that question now. We already know one of those laws, which says that the entropy is always increasing. If we have a hot thing and a cold thing, the heat goes from hot to cold. So the law of entropy is one such law. But we expect to understand the law of entropy from the point of view of mechanics. In fact, we have just been successful in obtaining all the consequences of the argument that heat cannot flow backwards by itself from just mechanical arguments, and we thereby obtained an understanding of the Second Law. Apparently we can get irreversibility from reversible equations. But was it only a mechanical argument that we used? Let us look into it more closely.
Since our question has to do with the entropy, our problem is to try to find a microscopic description of entropy. If we say we have a certain amount of energy in something, like a gas, then we can get a microscopic picture of it, and say that every atom has a certain energy. All these energies added together give us the total energy. Similarly, maybe every atom has a certain entropy. If we add everything up, we would have the total entropy. It does not work so well, but let us see what happens.
As an example, we calculate the entropy difference between a gas at a certain temperature at one volume, and a gas at the same temperature at another volume. For the change in entropy,
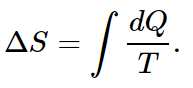
In the present case, the energy of the gas is the same before and after expansion, since the temperature does not change. So we have to add enough heat to equal the work done by the gas or, for each little change in volume,
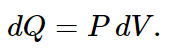
Putting this in for dQ, we get

as we obtained in Chapter 44. For instance, if we expand the volume by a factor of 2, the entropy change is Nk ln 2.
Let us now consider another interesting example. Suppose we have a box with a barrier in the middle. On one side is neon (“black” molecules), and on the other, argon (“white” molecules). Now we take out the barrier, and let them mix. How much has the entropy changed? It is possible to imagine that instead of the barrier we have a piston, with holes in it that let the whites through but not the blacks, and another kind of piston which is the other way around. If we move one piston to each end, we see that, for each gas, the problem is like the one we just solved. So we get an entropy change of Nk ln 2, which means that the entropy has increased by k ln 2 per molecule. The 2 has to do with the extra room that the molecule has, which is rather peculiar. It is not a property of the molecule itself, but of how much room the molecule has to run around in. This is a strange situation, where entropy increases but where everything has the same temperature and the same energy! The only thing that is changed is that the molecules are distributed differently.
We well know that if we just pull the barrier out, everything will get mixed up after a long time, due to the collisions, the jiggling, the banging, and so on. Every once in a while, a white molecule goes toward a black, and a black one goes toward a white, and maybe they pass. Gradually the whites worm their way, by accident, across into the space of blacks, and the blacks worm their way, by accident, into the space of whites. If we wait long enough, we get a mixture. Clearly, this is an irreversible process in the real world, and ought to involve an increase in the entropy.
Here we have a simple example of an irreversible process which is completely composed of reversible events. Every time there is a collision between any two molecules, they go off in certain directions. If we took a moving picture of a collision in reverse, there would be nothing wrong with the picture. In fact, one kind of collision is just as likely as another. So the mixing is completely reversible, and yet it is irreversible. Everyone knows that if we started with white and with black, separated, we would get a mixture within a few minutes. If we sat and looked at it for several more minutes, it would not separate again but would stay mixed. So we have an irreversibility which is based on reversible situations. But we also see the reason now. We started with an arrangement which is, in some sense, ordered. Due to the chaos of the collisions, it becomes disordered. It is the change from an ordered arrangement to a disordered arrangement which is the source of the irreversibility.
It is true that if we took a motion picture of this, and showed it backwards, we would see it gradually become ordered. Someone would say, “That is against the laws of physics!” So, we would run the film over again, and we would look at every collision. Everyone would be perfect, and every one would be obeying the laws of physics. The reason, of course, is that all molecule’s velocities are just right, so if the paths are all followed back, they get back to their original condition. But that is a very unlikely circumstance to have. If we start with the gas in no special arrangement, just whites and blacks, it will never get back.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|