Max Planck

Physics Is Finished

The first of the revolutionary quantum theorists we meet, Max Planck, would not have succeeded in revolutions of the other kind. Planck was born into the conservative society of nineteenth-century Prussia, and in his formal, disciplined way, he remained committed to the Prussian traditions, even in his scientific work, it seemed, throughout his life. Planck's life was devoted to an intense, sometimes desperate search a “hunger of the soul,” in Einstein's words for what was absolute and fundamental. “It is of paramount importance,” Planck wrote in his scientific autobiography, “that the outside world is something independent from man, something absolute, and the quest for the laws which apply to this absolute appeared to me as the most sublime scientific pursuit in life.” His faith in physics, ideally rooted in the principles of classical physics, as a manifestation of the absolute principles had the intensity of a religious belief. His intellectual strength and integrity, Einstein tells us, grew from an “emotional condition . . . more like that of a deeply religious man or a man in love; the daily effort is not dictated by either a purpose or a program, but by an immediate need.”

In one of those ironies that seems part of a trite novel, Planck was advised in 1875 when he was seventeen not to make a career in physics, particularly theoretical physics, because the significant work was finished except for the details. Planck took his own advice, however, and eventually made his way to Berlin, where he studied under two of Germany's most famous physicists, Hermann Helmholtz and Gustav Kirchhoff. The great scientists were less than inspiring in the lecture hall Helmholtz's lectures were poorly prepared, and Kirchhoff's were “dry and monotonous” but in their writings, and in the principles of their subject, thermodynamics, Planck found what he sought, “something absolute.”

By 1890, Planck had fully developed his ideas on thermodynamics and suffered some setbacks. Possibly because he chose to emphasize the then new concept of entropy, Planck found it nearly impossible at first to make a favorable impression, or any impression at all, on Germany's great thermodynamicists. Kirchhoff only found fault with Planck's papers, and Helmholtz did not bother to read them. Even Rudolf Clausius, who was responsible for the entropy concept that Planck used and refined, had no time for Planck or his papers. Another disappointment came when Planck discovered that much of his work on entropy theory had been anticipated by Willard Gibbs in America. Finally, in 1895, with help from his father, Planck received an academic appointment “as a message of deliverance” from the University of Kiel.

A few years later, Planck was still seeking broader professional recognition. He found it by entering a competition sponsored by the University of Gottingen, and, on a point related to electrical theory, innocently siding with Helmholtz against an antagonistic viewpoint held by Wilhelm Weber of Gottingen. Predictably, Planck's entry was refused first prize in the Gottingen competition, but with his work belatedly recognized by Helmholtz, Planck was in luck. In 1889, with Helmholtz supporting his candidacy, Planck was appointed as Kirchhoff's successor at the University of Berlin.

Blackbody Radiation

Max Planck's story as an unenthusiastic revolutionary began in about 1895 in Berlin, with Planck established as a theoretical physicist and concerned with the theory of the light and heat radiation emitted by special high-temperature ovens known in physical parlance as “blackbodies.” Formally, a blackbody is an object that emits its own radiation when heated, but does not reflect incident radiation. These simplifying features can be built into an oven enclosure by completely surrounding it with thick walls except for a small hole through which radiation escapes and is observed.

The color of radiation emitted by blackbody (and other) ovens depends in a familiar way on how hot the oven is: at 550^oC it appears dark red, at 750^oC bright red, at 900^oC orange, at 1000^oC yellow, and at 1200^oC and beyond, white. This radiation has a remarkably universal character: in a blackbody oven whose walls are equilibrated with the radiation they contain, the spectrum of the color depends exclusively on the oven's temperature. No matter what is in the oven, a uniform color is emitted that changes only if the oven's temperature is changed. A theory that partly accounted for these fundamental observations had been derived by Kirchhoff in 1859.

To Planck there were unmistakable signs here of “something absolute,” that sublime presence he had pursued in his thermodynamic studies. The blackbody oven embodied an idealized, yet experimentally accessible, instance of radiation interacting with matter. Blackbody theoretical work had been advancing rapidly because the experimental methods for analyzing blackbody spectra that is, the rainbow of emitted colors had been improving rapidly. The theory visualized a balanced process of energy conversions between the thermal energy of the blackbody oven's walls and radiation energy contained in the oven's interior. By the time Planck started his research, the blackbody radiation problem had developed into a theoretical tree with some obviously ripening plums.

Planck first did what theoreticians usually do when they are handed accurate experimental data: he derived an empirical equation to fit the data. His guide in this effort was a thermodynamic connection between the entropy and the energy of the blackbody radiation field. He defined two limiting and extreme versions of the energy entropy relation, and then guessed that the general connection was a certain linear combination of the two extremes. In this remarkably simple way, Planck arrived at a radiation formula that did everything he wanted. The formula so accurately reproduced the blackbody data gathered by his friends Heinrich Rubens and Ferdinand Kurlbaum that it was more accurate than the spectral data themselves: “The finer the methods of measurement used,” Planck tells us, “the more accurate the formula was found to be.”

The Unfortunate h

Max Born, one of the generation of theoretical physicists that followed Planck and helped build the modern edifice of quantum theory on Planck's foundations, looked on the deceptively simple maneuvers that led Planck to his radiation formula as “one of the most fateful and significant interpolations ever made in the history of physics; it reveals an almost uncanny physical intuition.” Not only was the formula a simple and accurate empirical one, useful for checking and correlating spectral data; it was, in Planck's mind, something more than that. It was not just a radiation formula, it was the radiation formula, the final authoritative law governing blackbody radiation. And as such it could be used as the basis for a theory even, as it turned out, a revolutionary one. Without hesitation, Planck set out in pursuit of that theory: “On the very day when I formulated the [radiation law],” he writes, “I began to devote myself to the task of investing it with true physical meaning.”

As he approached this problem, Planck was once again inspired by “the muse entropy,” as the science historian Martin Klein puts it. “If there is a single concept that unifies the long and fruitful scientific career of Max Planck,” Klein continues, “it is the concept of entropy.” Planck had devoted years to studies of entropy and the second law of thermodynamics, and a fundamental entropy energy relationship had been crucial in the derivation of his radiation law. His more ambitious aim now was to find a theoretical entropy energy connection applicable to the blackbody problem.

Ludwig Boltzmann interpreted the second law of thermodynamics as a “probability law.” If the relative probability or disorder for the state of a system was W, he concluded, then the entropy S of the system in that state was proportional to the logarithm of W,

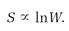
In a deft mathematical stroke, Planck applied this relationship to the blackbody problem by writing

S = kln W    (1)

for the total entropy of the vibrating molecules Planck called them “resonators”  in the blackbody oven's walls; k is a universal constant and W measures disorder. Although Boltzmann is often credited with inventing the entropy equation (1), and k is now called “Boltzmann's constant,” Planck was the first to recognize the fundamental importance of both the equation and the constant.

Planck came to this equation with reluctance. It treated entropy in the statistical manner that had been developed by Boltzmann. Boltzmann's theory taught the lesson that conceivably but against astronomically unfavorable odds any macroscopic process can reverse and run in the unnatural, entropy-decreasing direction, contradicting the second law of thermodynamics. Boltzmann's quantitative techniques even showed how to calculate the incredibly unfavorable odds. Boltzmann's conclusions seemed fantastic to Planck, but by 1900 he was becoming increasingly desperate, even reckless, in his search for an acceptable way to calculate the entropy of the blackbody resonators. He had taken several wrong directions, made a fundamental error in interpretation, and exhausted his theoretical repertoire. No theoretical path of his previous acquaintance led where he was certain he had to arrive eventually at a derivation of his empirical radiation law. As a last resort, he now sided with Boltzmann and accepted the probabilistic version of entropy and the second law.

For Planck, this was an “act of desperation,” as he wrote later to a colleague. “By nature I am peacefully inclined and reject all doubtful adventures,” he wrote, “but by then I had been wrestling unsuccessfully for six years (since 1894) with this problem of equilibrium between radiation and matter and I knew that this problem was of fundamental importance to physics; I also knew the formula that expresses the energy distribution in normal spectra [his empirical radiation law]. A theoretical interpretation had to be found at any cost, no matter how high.”

The counting procedure Planck used to calculate the disorder W in equation (1) was borrowed from another one of Boltzmann's theoretical techniques. He considered at least as a temporary measure that the total energy of the resonators was made up of small indivisible “elements,” each one of magnitude ε. It was then possible to evaluate W as a count of the number of ways a certain number of energy elements could be distributed to a certain number of resonators, a simple combinatorial calculation long familiar to mathematicians.

The entropy equation (1), the counting procedure based on the device of the energy elements, and a standard entropy energy equation from thermodynamics, brought Planck almost but not quite to his goal, a theoretical derivation of his radiation law. One more step had to be taken. His argument would not succeed unless he assumed that the energy ε of the elements was proportional to the frequency with which the resonators vibrated, ε 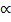 v, or

ε = hv,    (2)

with h a proportionality constant. If he expressed the sizes of the energy elements this way, Planck could at last derive his radiation law and use the blackbody data to calculate accurate numerical values for his two theoretical constants h and k.

This was Planck's theoretical route to his radiation law, summarized in a brief report to the German Physical Society in late 1900. Planck hoped that he had in hand at last the theoretical plum he had been struggling for, a general theory of the interaction of radiation with matter. But he was painfully aware that to reach the plum he had ventured far out on a none-too-sturdy theoretical limb. He had made use of Boltzmann's statistical entropy calculation an approach that was still being questioned. And he had modified the Boltzmann technique in ways that modern commentators have found questionable. Abraham Pais, one of the best of the recent chroniclers of the history of quantum theory, says that Planck's adaptation of the Boltzmann method “was wild.”

Even wilder was Planck's use of the energy elements ε in his development of the statistical argument. His procedure required the assumption that energy, at least the thermal energy possessed by the material resonators, had an inherent and irreducible graininess embodied in the ε quantities. Nothing in the universally accepted literature of classical physics gave the slightest credence to this idea. The established doctrine to which Planck had previously adhered as faithfully as anyone was that energy of all kinds existed in a continuum. If a resonator or anything else changed its energy, it did so through continuous values, not in discontinuous packets, as Planck's picture suggested.

In Boltzmann's hands, the technique of allocating energy in small particle-like elements was simply a calculational trick for finding probabilities. In the end, Boltzmann managed to restore the continuum by assuming that the energy elements were very small. Naturally, Planck hoped to avoid conflict with the classical continuum doctrine by taking advantage of the same strategy. But to his amazement, his theory would not allow the assumption that the elements were arbitrarily small; the constant h in equation (2) could not be given a zero value.

Planck hoped that the unfortunate h, and the energy structure it implied, were unnecessary artifacts of his mathematical argument, and that further theoretical work would lead to the result he wanted with less drastic assumptions. For about eight years, Planck persisted in the belief that the classical viewpoint would eventually triumph. He tried to “weld the [constant] h somehow into the framework of the classical theory. But in the face of all such attempts this constant showed itself to be obdurate.” Finally Planck realized that his struggles to derive the new physics from the old had, after all, failed. But to Planck this failure was  thorough enlightenment. . . . I now knew for a fact that [the energy elements] . . . played a far more significant part in physics than I had originally been inclined to suspect, and this recognition made me see clearly the need for introduction of totally new methods of analysis and reasoning in the treatment of atomic problems.”

The physical meaning of the constant h was concealed, but Planck did not have much trouble extracting important physical results from the companion constant k. By appealing to Boltzmann's statistical calculation of the entropy of an ideal gas, he found a way to use his value of k to calculate Avogadro's number, the number of molecules in a standard or molar quantity of any pure substance. The calculation was a far better evaluation of Avogadro's number than any other available at the time, but that superiority was not recognized until much later. Planck's value for Avogadro's number also permitted him to calculate the electrical charge on an electron, and this result, too, was superior to those derived through contemporary measurements.

These results were as important to Planck as the derivation of his radiation law. They were evidence of the broader significance of his theory, beyond the application to blackbody radiation. “If the theory is at all correct,” he wrote at the end of his 1900 paper, “all these relations should be not approximately, but absolutely, valid.” In the calculation of Avogadro's number and the electronic charge, Planck could feel that his theory had finally penetrated “to something absolute.”

In part because of Planck's own sometimes ambivalent efforts, and in part because of the efforts of a new, less inhibited scientific generation, Planck's theory stood firm, energy discontinuities included. But the road to full acceptance was long and tortuous. Even the terminology was slow to develop. Planck's energy “elements” eventually became energy “quanta,” although the Latin word  “quantum,” meaning quantity, had been used earlier by Planck in another context. Not until about 1910 did Planck's theory, substantially broadened by the work of others, have the distinction of its formal name, “quantum theory.”

Einstein’s Energy Quanta (Photons)

One of the few perceptive readers of Planck's early quantum theory papers was the junior patent examiner in Bern, Albert Einstein. To Einstein, the postulate of the energy elements was vivid and real, if appalling, “as if the ground had been pulled from under one, with no firm foundation seen anywhere upon which one could have built.” As it happened, the search for a “firm foundation” occupied Einstein for the rest of his life. But even without finding a satisfying conceptual basis, Einstein managed to discover a powerful principle that carried the quantum theory forward in its next great step after Planck's work. He presented his theory in one of the papers published during his “miraculous year” of 1905.

Planck was cautious in his use of the quantum concept. For good reason, considering its radical implications, he had hesitated to regard the quantum as a real entity. And he was careful not to infer anything concerning the radiation field, partly light and partly heat radiation, contained in the blackbody oven's interior. The energy quanta of which he spoke belonged to his resonator model of the vibrating molecules in the oven's walls. Einstein, in one of his 1905 papers, and in several subsequent papers, presented the “heuristic” viewpoint that real quanta existed and that they were to be found, at least in certain experiments, as constituents of light and other kinds of radiation fields. He stated his position with characteristic clarity and boldness: “In accordance with the assumption to be considered here, the energy of a light ray . . . is not continuously distributed over an increasing space but consists of a finite number of energy quanta which are localized in space, which move without dividing, and which can only be produced and absorbed as complete units.”

Although it was hedged with the adjective “heuristic,” the picture Einstein presented was attractively simple: the energy contained in radiation fields, particularly light, was not distributed continuously but was localized in particle like entities. Einstein called these particles of radiation “energy quanta”; in modern usage, complicated by the changing fortunes of Einstein’s theory, they are called “photons.”

Einstein developed his concept of photons in a variety of short, clever arguments written somewhat in the style of Planck's 1900 paper. The entropy concept and fundamental equations from thermodynamics again opened the door to the quantum realm. Entropy equations for a radiation field make the field look like an ideal gas containing a large but finite number of independent particles. Each of these radiation particles photons, in modern parlance carries an amount of energy given by one of Planck's energy elements hv, with v now representing a radiation frequency. If there are N photons, the total energy is

   E = Nhv.   (3)

Einstein drew from this equation the conclusion that the radiation field, like the ideal gas, contains N independent particles, the photons, and that the energy of an individual photon is

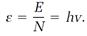
No doubt Einstein was convinced by this reasoning, but it is not certain that anyone else in the world shared his convictions. The year was 1905. Planck's quantum postulate was still generally ignored, and Einstein had now applied it to light and other forms of radiation, a step Planck himself was unwilling to take for another ten years. What bothered Planck, and anyone else who read Einstein's 1905 paper, was that the concept of light in particulate form had not been taken seriously by physicists for almost a century. The optical theory prevailing then, and throughout most of the nineteenth century, pictured light as a succession of wave fronts bearing some resemblance to the circular waves made by a pebble dropped into still water. It had been assumed ever since the work of Thomas Young and Augustin Fresnel in the early nineteenth century that light waves accounted for the striking interference pattern of light and dark bands generated when two specially prepared light beams are brought together. Other optical phenomena, particularly refraction and diffraction, were also simply explained by the wave theory of light.

One hundred years after Young's first papers, Albert Einstein was rash enough to suggest that there might be some heuristic value in returning to the observation once proposed by Newton, that light can behave like a shower of particles. Einstein had found particles of light in his peculiar use of the quantum postulate. And, more important, he also showed in one of his 1905 papers that experimental results offered impressive evidence for the existence of particles of light, in astonishing contradiction to previous experiments that stood behind the seemingly impregnable wave theory.

The most important experimental evidence cited by Einstein concerned the   “photoelectric effect,” in which an electric current is produced by shining ultraviolet light on a fresh metal surface prepared in a vacuum. In the late 1890s and early 1900s, this photoelectric current was studied by Philipp Lenard (the same Lenard who later conceived a rabid, anti-Semitic hatred for Einstein, and worked furiously in the ultimately successful campaign to drive Einstein from Germany). Lenard discovered that the current emitted by the illuminated “target” metal consists of electrons whose kinetic energy can accurately be measured, and that the emitted electrons acquire their energy from the light beam shining on the metallic surface. If the classical viewpoint is taken that light waves beat on the metallic surface like ocean waves, and that electrons are disturbed like pebbles on a beach it seems necessary to assume that each electron receives more energy when the illumination is more intense, when the waves strike with more total energy. This, however, is not what Lenard found; in 1902, he discovered that, although the total number of electrons dislodged from the metallic surface per second increases in proportion to the intensity of the illumination, the individual electron energies are independent of the light intensity.

Einstein showed that this puzzling feature of the photoelectric effect is comprehensible once the illumination in the experiment is understood to be a collection of particle like photons. He proposed a simple mechanism for the transfer of energy from the photons to the electrons of the metal: “According to the concept that the incident light consists of [photons] of magnitude hv . . . one can conceive of the ejection of electrons by light in the following way. [Photons] penetrate the surface layer of the body [the metal], and their energy is transformed, at least in part, into kinetic energy of electrons. The simplest way to imagine this is that a [photon] delivers its entire energy to a single electron; we shall assume that is what happens.”

Each photon, if it does anything measurable, is captured by one electron and transfers all its energy to that electron. Once an electron captures a photon and carries away as its own kinetic energy the photon’s original energy, the electron attempts to work its way out of the metal and contribute to the measured photo electric current. As an electron edges its way through the crowd of atoms in the metal, it loses energy, so it emerges from the metal surface carrying the captured energy minus whatever energy has been lost in the metal. If the energy that the metal erodes from an electron is labeled P, if the captured photon's original energy, also the energy initially transferred to the electron, is represented with Planck's hv (v is now the frequency of the illuminating ultraviolet light), and if energy is conserved in the photoelectric process, the energy E of an electron emerging from the target can be written

  E = hv - P.    (4)

Einstein's picture of electrons being bumped out of metal targets in single photon electron encounters easily explains the anomaly found by Lenard. Each interaction leads to the same photon to electron energy transfer, regardless of light intensity. Therefore electrons joining the photoelectric current from some definite part of the metallic target have the same energy whether just one or countless photons strike the metal per second. Although admirably simple, this explanation must have seemed almost as far-fetched to Einstein's skeptical audience as the rest of his arguments. The rule that one photon is captured by one electron “not only prohibits the killing of two birds by one stone,” as the British theorist James Jeans remarked, “but also the killing of one bird by two stones.”

More than anything else Einstein achieved in physics, his photon theory was treated with distrust and skepticism. Not until 1926 was the now standard term         “photon” introduced by Gilbert Lewis. What was obvious to Einstein by simply exercising his imagination and intuition was still being seriously questioned twenty years later. It took something approaching a mountain of evidence to make a permanent place for photons in the world of quantum theory.

While Einstein was beginning his bold explorations of the quantum realm, Planck was becoming the chief critic of his own theory. Planck seems to have had no regrets perhaps he was pleased that the work of building quantum theory had passed to Einstein and a new generation. Late in his life he wrote, with no sense of the personal irony, “A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because . . . a new generation grows up that is familiar with it.”