Paul Dirac

Three Brands of Quantum Mechanics

When Dirac emerged from his studies under Fowler, and began to scrutinize the rapidly developing world of quantum mechanics, he found what appeared to be two different methods. On the one hand, there was the matrix mechanics espoused by the Gottingen school (Heisenberg, Born, and Jordan), and on the other hand, the wave mechanics of Schrodinger in Zurich. The matrix method works with tables of numbers (matrices) and follows certain rules of algebra involving addition, subtraction, multiplication, inversion, transformation, and so forth. Wave mechanics is rooted in calculus; its master equation, named after Schrodinger, is an energy equation formulated as a differential equation.

To Dirac, this was mathematically unacceptable: quantum mechanics did not need two voices. Matrix mechanics and wave mechanics treated the same problems and provided the same answers. They had to be representations of a single, more elegant mathematical language. Dirac first focused on Heisenberg's strange multiplication rule that xy does not equal yx for the matrices of his mechanics, that is, xy - yx does not equal zero. The “commutator” xy - yx, which Dirac represented with a bracket symbol,

                                     [x, y] = xy - yx,

has a certain formal resemblance to a mathematical entity called a “Poisson bracket” used by nineteenth-century theorists to put Newton's mechanics in a particularly concise and general form. In his first major paper, published in 1925, Dirac presented a striking correspondence between classical mechanics written with Poisson brackets and quantum mechanics expressed with his own bracket notation. Others were traveling this theoretical path, but none with Dirac's mastery. Max Born was astonished when he saw the paper. “The name Dirac was completely unknown to me,” he recalled later. “The author appeared to be a youngster, yet everything was perfect in its way and admirable.” Heisenberg's admiration came more grudgingly. In a letter to Pauli he wrote, “An Englishman working with Fowler, Dirac, has independently re-done the mathematics for my work. Born and Jordan will probably be a bit depressed about that, but at any rate they did it first and now we really know that the theory is correct.”

The “youngster” soon had much more to say. In 1926, he took quantum mechanics to the higher mathematical plane that he knew existed beyond matrix mechanics and wave mechanics. This was his “transformation theory.” It showed, in broad terms, how to transform from one version of quantum mechanics to another, and demonstrated that whether one chose matrix mechanics or wave mechanics was simply a matter of taste or expedience.

In his transformation theory, Dirac revealed the logical essence of quantum mechanics, and he was proud of it. “This work [transformation theory] gave me more pleasure in carrying it through than any of the other papers which I have written on quantum mechanics either before or after,” he wrote later.

Out of the Sky

Dirac's habit of working in isolation left his colleagues, even those at Cambridge, wondering what would come next. Nevill Mott, as close as anyone to Dirac, remarked that “all Dirac's discoveries just sort of fell on me and there they were. I never heard him talk about them. . . . They just came out of the sky.” In 1928, from out of the sky, came what most commentators rate as Dirac's greatest contribution to physics: his relativistic theory of the electron.

Schrodinger had supplied a preliminary theory of electron behavior with his differential equation, but the equation had two serious faults: as an energy equation, it did not follow the dictates of Einstein's special theory of relativity, and it took no notice of spin motion, which by 1925 had become an accepted electron attribute, as important as the electron's mass and charge. It was suspected that somehow relativity and spin were connected, but no one had even come close to uncovering the connection.

We can glimpse the energy problem by looking closer at Schrodinger's equation. For a free electron (outside the confines of the atom), it calculates the electron's kinetic energy in terms of its momentum. In Newton's mechanics, the kinetic energy E of a particle is calculated from the particle's mass m and speed v with

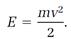
The momentum p of the particle is the product of the mass and speed,

   p = mv,

so

 (1)

Schrodinger supplied rules that translated this classical equation into a quantum mechanical equation that describes free electrons. The form of Schrodinger's equation for this case is

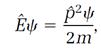 (2)

in which ψ is another fundamental ingredient of quantum mechanics, the wave function; pˆ 2ψ and Ế ψ denote certain derivatives which need not be specified in detail here. Equation (2) is a differential equation; when it is solved, it supplies information on both the energy and the wave function of the free electron.

Special relativity theory does not accept the energy equation (1), or anything remotely like it. The relativistic energy equation for a free electron is

 (3)

with c equal to the speed of light. Note that the energy E is squared in the relativistic equation (3), but not in the nonrelativistic equation (1). This seemingly innocent mathematical feature had far-reaching consequences. It eventually opened the door to a new realm of physics.

Several of Dirac's contemporaries investigated the differential equation derived directly from the energy equation (3), in the same way Schrodinger had derived his successful equation (2) from the classical equation (1). Such an equation has the form

 (4)

another differential equation.

Dirac saw a subtle difficulty in this equation: it was not sanctioned by his transformation theory, and that for him was a fatal flaw. “The transformation theory had become my darling,” he wrote later. “I was not interested in considering any theory which would not fit my darling. . . . I just couldn’t face giving up the transformation theory.” He found harmony with his transformation theory by simply taking the square root of equation (3), thus eliminating the E² on the left,

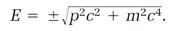 (5)

This is actually two equations, as indicated by the ± notation,

 (6)

Either of these equations squared gives equation (3) (the square of a negative number yields a positive number).

Dirac's task, as he saw it, was to invent a differential equation in the image of the relativistic equation (5), following as much as possible the rules that had served Schrodinger so well. It was a formidable undertaking, requiring much mathematical ingenuity, “playing with equations and seeing what they give,” as Dirac put it. After about two months of this, Dirac had what he wanted. In its most elegant form, Dirac's relativistic electron equation (which appears as the title to this chapter) is

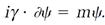 (7)

It is appropriately carved on the Dirac memorial in Westminster Abbey.

Like some other grand equations of theoretical physics (for instance, Einstein's gravitational field equation), Dirac's electron equation (7) is not so simple as it looks. All of the differential aspects of the equation are compressed into the symbol ∂; the factor γ represents four 4×4 arrays of numbers (matrices); and ψ, no longer the simple wave function of Schrodinger's theory, now has four components. The symbol i is a ubiquitous mathematical symbol representing the constant . To make calculations easier, the units for equation (7) are chosen so the speed of light c, an inconveniently large number in ordinary units, and Planck's constant h, an inconveniently small number, both have a value of one.

Equation (7) describes a free electron, unaffected by an external field. When the equation is elaborated so it includes the influence of an applied electromagnetic field, a truly astonishing thing happens: the equation reveals, with no ad hoc prompting from the theorist, that electrons have spin motion. Here was elegant proof of the prevailing suspicion that relativity and spin were connected.

If some of Dirac's contemporaries failed to see the importance of his transformation theory, few had reservations about his relativistic electron theory. “[It] was regarded as a miracle,” Leon Rosenfeld, one of Bohr’s associates, recalled. “The general feeling was that Dirac had more than he deserved! Doing physics in that way was not done! . . . It [the Dirac equation] was immediately seen as the solution. It was regarded as an absolute wonder.” The miracle it performed was the deduction of electron spin motion. Previous theories had done no better than to graft the spin concept onto the Schrodinger equation more or less as an afterthought.

The ± Difficulty

But there was a price to be paid. Although Dirac's equation answered longstanding questions about electron spin, it raised a profoundly puzzling further question begged by the ± in the energy equation (5). The equation tells us that both positive and negative energies are allowed, but before Dirac's work, negative energies had had no place in relativity theory. In some cases, physicists avoid problems like this by simply discarding mathematically valid, but physically meaningless, quantities. That was not a way out of what became to be known as the “± difficulty,” however, because Dirac's theory permitted electrons to make transitions from positive to negative energy states and vice versa. Like it or not, the negative energy states had to remain in the picture. There was a continuum of positive energy states beginning at m₀c² (for p = 0 in equation [5] with the ± sign in effect); m₀ is the electron mass when the electron is at rest. Mirroring these is a continuum of negative energy states beginning at -m₀c² (also for p = 0). See figure 1.1.

Dirac proposed a radical solution to the ± problem. He supposed that all the negative energy states were occupied by a “sea” of electrons according to the Pauli principle, one and only one electron to each state. If, in addition, some electrons also occupied positive energy states, they could not make transitions to the already completely occupied negative energy states, and would thus behave normally. Dirac supposed further that if energy were available, say in the form of a γ-ray photon, an electron could be promoted from a negative energy state to a positive one, where it became an observable positive-energy electron, leaving behind in the sea of negative-energy electrons a vacancy, a “hole,” which

Figure 1.1. Positive and negative energy states according to the relativistic energy equation (5).

gave rise to observable physical effects (see fig. 1.2). What kind of physical effects? Because a one-electron hole was an absence of negative charge, it had an effective positive charge. That charge was +e if positive-energy electrons had the charge -e.

The charge on the proton is also +e, so Dirac proposed first that holes in the sea of negative-energy electrons were observable and that they were protons. It was an appealing idea. If acceptable, it meant that Dirac's theory explained both of the elementary particles known at the time, the electron and the proton. But it did not survive the critics. Robert Oppenheimer pointed out that an ordinary piece of matter would, according to Dirac's theory, annihilate itself in 10^-10 second as electrons fell into proton holes, the downward transition being accompanied by the emission of γ-ray photons (the reverse of the process shown in fig. 1.2). Pauli was prompted to announce his “second principle,” to the effect that any theory should first be tested by applying it to the theorist who invented it. Pauli's test would have been spectacularly negative when applied to Dirac and his theory: in 10^-10 second theorist Dirac would have disappeared in a burst of γ rays.

But Dirac had the last laugh. In 1931, he changed his mind and identified the holes as a new kind of elementary particle, an electron with a positive charge, which he called an “antielectron.” While he was at it, he speculated that “antiprotons,” protons with negative charges, also existed. That same year

Figure 1.2. A negative-energy electron promoted to a positive-energy state by the absorption of a γ-ray photon.

Carl Anderson, a research fellow at the California Institute of Technology (Caltech), published strong experimental evidence for the existence of Dirac's antielectrons. Anderson was studying the energies of secondary electrons produced by cosmic radiation reaching Earth from outer space. His apparatus was a Wilson cloud chamber. He expected that his cloud chamber photographs would show secondary electrons of the kind described by Arthur Compton. He soon found that he was wrong, however; most of the secondary electrons were positively charged.

Anderson naturally assumed that the positive particles were protons, but this assumption was not supported by the cloud chamber tracks, which showed properties belonging to particles much less massive than protons. In 1933, Anderson reported the discovery of positive electrons, with the same physical properties as Dirac's antielectrons. Anderson called them “positrons.”

According to Dirac's theory, positrons form in the process shown in figure 1.2, when negative-energy electrons absorb energy from one of the components of the cosmic radiation, perhaps γ rays, and are promoted to positive energy states. Because the hole or positron creating events are rare, the density of holes is sparse, and the loss of electrons by falling into holes is no longer the disaster it was with Dirac's identification of the holes as protons. But each individual electron hole that is, electron-positron encounter is a disaster for the electron and positron involved, because both particles lose their identities in the process and two γ-ray photons appear in their place (see fig. 1.3).

Although Anderson was familiar with Dirac’s theory, he writes that “the discovery of the positron was wholly accidental.” Dirac's theory, which could have guided any “sagacious” experimentalist to “discover the positron in a single afternoon . . . [in] any well-equipped laboratory . . . played no part whatsoever in the discovery of the positron.” Like Planck's quantized blackbody resonators, Einstein's light quanta (photons), Bohr's stationary states, and de Broglie's matter waves, Dirac's sea of negative energy states and the holes it contains were at first too “unphysical” for most physicists to accept them with confidence.

Anderson's positron discovery was the first in a long series of antiparticle discoveries, including (in 1955) the antiproton and antineutron. Physicists are now convinced that all particles, elementary and otherwise, have their antiparticle counterparts. And it is conceivable that our universe, or another, contains entire antiworlds built of antimatter.

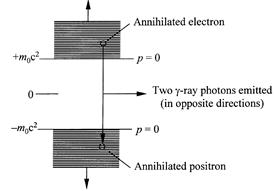
Figure 1.3. Annihilation of a positron and an electron resulting in formation of γ-rays.