William Thomson

A Problem Solver

William Thomson was many things physicist, mathematician, engineer, inventor, teacher, political activist, and famous personality but before all else he was a problem solver. He thrived on scientific and technological problems of all kinds. Whatever the problem, abstract or applied, Thomson usually had an original insight and a valuable solution. As a scientist and technologist, he was a virtuoso.

       Even Helmholtz, another famous problem solver, was amazed by Thomson's virtuosic performances. After meeting Thomson for the first time, Helmholtz wrote to his wife, “He far exceeds all the great men of science with whom I have made personal acquaintance, in intelligence and lucidity, and mobility of thought, so that I felt quite wooden beside him sometimes.” Helmholtz later wrote to his father, “He is certainly one of the first mathematical physicists of his day, with powers of rapid invention such as I have seen in no other man.”

       Thomson and Helmholtz became good friends, and in later years Thomson made their discussions on subjects of mutual interest into an extended competition, which we can assume Thomson usually won. On one occasion, when Helmholtz was visiting on board Thomson's sailing yacht in Scotland, the subject for marathon discussion was the theory of waves, which, as Helmholtz wrote (again in a letter to his wife), “he loved to treat as a kind of race between us.” When Thomson had to go ashore for a few hours, he told his guest, “Now mind, Helmholtz, you're not to work at waves while I’m away.”

     Much of Thomson's problem-solving talent was based on his extraordinary mathematical aptitude. He must have been a mathematical prodigy. While in his teens, he matriculated at the University of Glasgow (where his father was a professor of mathematics) and won prizes in natural philosophy and astronomy. When he was sixteen he read Joseph Fourier's Analytical Theory of Heat, and correctly defended Fourier's mathematical methods against the criticism of Philip Kelland, professor of mathematics at the University of Edinburgh. This work was published in the Cambridge Mathematical Journal in 1841, the year Thomson entered Cambridge as an undergraduate. By the time he graduated, Thomson had published twelve research papers, all on topics in pure and applied mathematics. Most of the papers were written under the pseudonym “P.Q.R.,” since it was considered unsuitable for an undergraduate to spend his time writing original papers.

        Another element of Thomson's talent that certainly contributed to his success was his huge, single-minded capacity for hard work. He wrote 661 papers and held patents on 69 inventions. Every year between 1841 and 1908 he published at least two papers, and sometimes as many as twenty-five. He carried proofs and research notebooks wherever he traveled and worked on them whenever the spirit moved him, which evidently was often. Helmholtz wrote (in another of his lively letters to his wife) of life on board the Thomson yacht when the host had “calculations” on his mind:

W. Thomson presumed so far on the freedom of his surroundings that he carried his mathematical note-books about with him, and as soon as anything occurred to him, in the midst of company, he would begin to calculate, which was treated with a certain awe by the party. How would it be if I accustomed the Berliners to the same proceedings? But the greatest naivete of all was when on Friday he had invited all the party to the yacht, and then as soon as the ship was on her way, and every-one was settled on deck as securely as might be in view of the rolling, he vanished into the cabin to make calculations there, while the company were left to entertain each other so long as they were in the vein; naturally they were not exactly very lively.

      Thomson may not have been a considerate host, but he was able to work with great effectiveness within the scientific, industrial, and academic establishments of his time. He became a professor of natural philosophy at the University of Glasgow when he was twenty-one. One of his first scientific accomplishments was the founding of the first British physical laboratory. His researches quickly became famous, not only in Britain but also in Europe. At the age of twenty seven, he was elected to fellowship in the Royal Society. By the time he was thirty-one, he had published 96 papers, and his most important achievements in physics and mathematics were behind him.

        In 1855, he embarked on a new career, one for which his talents were, if anything, more spectacularly suited than for scientific research; he became a director of the Atlantic Telegraph Company, formed to accomplish the Herculean task of laying and operating a telegraph cable spanning two thousand miles across the Atlantic Ocean from Ireland to Newfoundland. The cable became one of the world's technological marvels, but without Thomson's advice on instrument design, and on cable theory and manufacture, it might well have been a spectacular failure.

        After the Atlantic cable saga, which went on for ten years before its final success, Thomson's fame spread far beyond academic and scientific circles. He was the most famous British scientist, as Helmholtz was later to become the most famous German scientist. Income from the cable company and from his inventions made him wealthy, and he managed his investments wisely. In 1866, the year the cable project was completed, Thomson was knighted. In 1892, partly for political reasons he was active in the Liberal Unionist Party, which opposed home rule for Ireland he was elevated to the peerage, as Baron Kelvin of Largs. (Largs, a small town on the Firth of Clyde, was the location of Thomson's estate, Nether all; the River Kelvin flows past the University of Glasgow.)

       As one of his biographers, Silvanus Thompson, tells us, Thomson was “a man lost in his work.” But he was a devoted husband and family member. He was always close to his father, his sister Elizabeth, and his brother James, an engineering professor who shared his interest in thermodynamics. He was married twice. His first wife, Margaret Crum, was an invalid throughout the marriage, in need of frequent attention, which Thomson gave generously. Her death in 1870 was a severe blow. A few years later he married Frances Blandy, always called “Fanny,” the daughter of a wealthy Madeira landowner. The second marriage was as blessed as the first was tragic. Fanny was gregarious and gifted; she became an efficient manager of the Thomson household and found a rich social life in Glasgow as the second Lady Thomson and then as Lady Kelvin.

The Thermometry Problem

At the same time he was struggling with these problems, Thomson was investigating another aspect of the Carnot legacy, the temperature-dependent function that Carnot labeled F. Thomson represented the function with μ and called it “Carnot's function.” He suggested that the two fundamental properties of the function that it was dependent only on temperature, and that in all determinations it had the same mathematical form be used to define a new absolute temperature scale.

        Previously, absolute temperatures had been expressed on a scale based on an idealization of gas behavior. If the temperature is held constant, the volume V of an ideal gas decreases as the pressure increases,

If the pressure is held constant, the ideal gas volume increases as the temperature increases,

with T representing temperature measured on an absolute scale that begins at zero and does not allow negative values. Combining the two proportionalities into one, we have in general

or

      (1)

The constant in this equation, since it is a constant, can be determined by measuring P and V at any temperature T. Customarily, the temperature of an ice water mixture (0^oC) is chosen. If P₀, V₀ and T₀ are measured at that temperature, equation (1) evaluates the constant as

so

      (2)

How is the absolute temperature T related to the ordinary temperature t measured, say, on the Celsius scale? Assume that the two scales differ by a constant

a, that

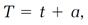       (3)

and substitute this in equation (2) to obtain

 (4)

     The expansion of a gas with increasing temperature, expressed mathematically by the derivative dV/dt, is measurable. This derivative divided by the volume V itself defines the “expansion coefficient” α, also measurable,

According to this, and equation (4) applied with P = P₀,

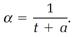 (5)

Thus a measured value of the expansion coefficient α at a known temperature evaluates the constant a in equation (3) and completes the definition of absolute temperature. Around the turn of the nineteenth century, Joseph Gay-Lussac and John Dalton independently measured α for several gases and found a value of about 267 for the constant a expressed on the Celsius scale; the corresponding modern value is 273. At zero absolute temperature T = 0, and according to equation (3), the Celsius temperature is t = -a = -273^oC.

       Thomson was not satisfied with this treatment of the absolute-temperature scale. He objected that it was not a satisfactory basis for a general theory of temperature. Real gases were never actually ideal, he argued, and that meant special elaborations of the gas law, a different one for each gas, had to be determined for accurate temperature measurements: there was no universal gas law for real gases. Carnot's function, on the other hand, had just the universality real gas laws lacked; it was always the same no matter what material was used for its determination.

         Thomson proposed that Carnot's function be used as a basis for a new temperature scale. He stated this concept as a principle of absolute thermometry in 1848. His basic idea, as he put it later, was that “Carnot's function (derivable from the properties of any substance whatever, but the same for all bodies at the same temperature), or any arbitrary function of Carnot's function, may be defined as temperature and is therefore the foundation of an absolute system of thermometry.” Thomson made two suggestions concerning the appropriate function, one in 1848 later abandoned, and another in 1854. Thomson did not find it easy to make up his mind on this thermometry problem. His final decision was not made until other aspects of his theory of heat had been settled. The main obstacle to progress was still another aspect of the Carnot-Joule dilemma. Thomson found ways to derive equations from Carnot's theory that could be used to calculate Carnot’s function μ, and in 1849 he prepared an extensive table of μ values. At first, this calculation had Thomson's full confidence, based as it was on the authority of Carnot's theory, but there was one loose end that he could not ignore. Joule had suggested, in a letter to Thomson in 1848, that Carnot's function was proportional to the reciprocal of the temperature according to

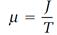 (6)

in which the temperature T is determined on the ideal-gas absolute scale, and J is Joule's mechanical equivalent of heat. At about the same time, Helmholtz reached the same conclusion, but his work was not yet known in Britain. When Thomson made comparisons between his calculations and those based on Joule's equation (6), he could get no better than approximate agreement. Again he was confronted by a problem brought on by Joule's challenge to Carnot's theory.

      Joule was inclined to think, correctly, that there were errors in the data used by Thomson in calculating his table of μ values.

The Thermometry Problem Solved

With the publication of his paper on the energy dissipation principle, Thomson could feel that he had finally brought together in harmony the concepts of Joule, Carnot, and Fourier. But the fundamentals of his thermodynamics were still not quite complete. He had not yet made a decision about the nagging thermometry problem that had been bothering him for almost five years. The specific problem was how to relate the temperature-dependent Carnot's function μ to absolute temperature.

       I lack the space here to give a complete account of Thomson's work on this stubborn and frustrating problem. Thomson had hoped to be able to use equations he had derived from Carnot's theory to calculate values of Carnot's function μ. Eventually he had to admit defeat in this effort when he found that some assumptions used in the calculation were not valid. Thomson enlisted Joule's help in another, more elaborate attempt to calculate μ values. The principal aim of the Joule-Thomson work was to study real (non-ideal) gas behavior, and in this it succeeded. But Thomson also tried to use Joule's data to calculate μ values, and once again he failed to muster the calculational wherewithal to complete the task.

       Finally, in 1854, Thomson decided to take a different tack in his pursuit of the still-elusive Carnot function. He returned to his 1848 thermometry principle, which asserted that Carnot's function, or any function of Carnot's function, could be used as a basis for defining an absolute-temperature scale. No doubt influenced by the Joule evaluation of Carnot's function in equation (6), he defined a new absolute-temperature scale that had this same form. Representing temperatures on this scale T, his assumption was

 (7)

He also assumed that the degree on the new scale is equivalent to the degree on the Celsius scale. Even if Carnot's function μ could not be calculated accurately with the data then available, Thomson was sure that it would eventually be calculated, and that his thermometry principle was secure. The principle permitted any assumed mathematical relation between the absolute temperature and μ. Thomson could see that equation (6), one of the simplest possible choices, and in agreement with the ideal-gas absolute-temperature scale, was acceptable and the best choice. Thomson was rewarded for his labors on the absolute temperature scale: the modern unit of absolute temperature is called the “kelvin” (lowercase), abbreviated “K” (uppercase).