Clenshaw Recurrence Formula
المؤلف:
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
المصدر:
"Recurrence Relations and Clenshaw,s Recurrence Formula." §5.5 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press,
الجزء والصفحة:
pp. 172-178
9-12-2021
1283
Clenshaw Recurrence Formula
The downward Clenshaw recurrence formula evaluates a sum of products of indexed coefficients by functions which obey a recurrence relation. If
 |
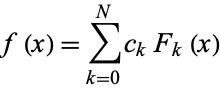(1)
|
and
 |
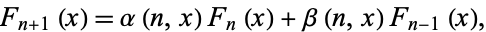(2)
|
where the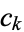 
s are known, then define
for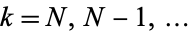 
and solve backwards to obtain 
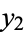and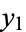 
.
 |
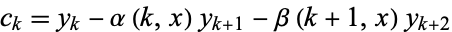(5)
|
The upward Clenshaw recurrence formula is
 |
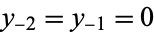(11)
|
![y_k=1/(beta(k+1,x))[y_(k-2)-alpha(k,x)y_(k-1)-c_k]](https://mathworld.wolfram.com/images/equations/ClenshawRecurrenceFormula/NumberedEquation5.gif) |
(12)
|
for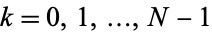 
.
 |
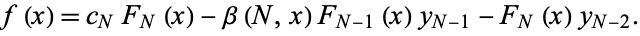(13)
|
REFERENCES:
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Recurrence Relations and Clenshaw's Recurrence Formula." §5.5 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 172-178, 1992
الاكثر قراءة في التحليل العددي
اخر الاخبار
اخبار العتبة العباسية المقدسة
