


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-11-2020
Date: 1-11-2020
Date: 20-8-2020
|
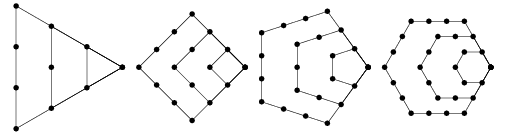
A polygonal number is a type of figurate number that is a generalization of triangular, square, etc., to an 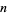 -gon for
-gon for 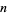 an arbitrary positive integer. The above diagrams graphically illustrate the process by which the polygonal numbers are built up. Starting with the
an arbitrary positive integer. The above diagrams graphically illustrate the process by which the polygonal numbers are built up. Starting with the 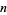 th triangular number
th triangular number 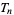 , then
, then
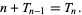 |
(1) |
Now note that
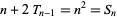 |
(2) |
gives the 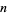 th square number,
th square number,
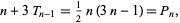 |
(3) |
gives the 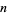 th pentagonal number, and so on. The general polygonal number can be written in the form
th pentagonal number, and so on. The general polygonal number can be written in the form
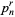 |
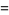 |
![1/2n[(n-1)r-2(n-2)]](https://mathworld.wolfram.com/images/equations/PolygonalNumber/Inline9.gif) |
(4) |
 |
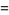 |
![1/2n[(r-2)n-(r-4)],](https://mathworld.wolfram.com/images/equations/PolygonalNumber/Inline12.gif) |
(5) |
where 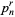 is the
is the 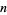 th
th 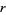 -gonal number (Savin 2000). For example, taking
-gonal number (Savin 2000). For example, taking 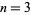 in (5) gives a triangular number,
in (5) gives a triangular number, 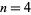 gives a square number, etc.
gives a square number, etc.
Polygonal numbers are implemented in the Wolfram Language as PolygonalNumber.
Call a number  -highly polygonal if it is
-highly polygonal if it is  -polygonal in
-polygonal in  or more ways out of
or more ways out of  , 4, ... up to some limit. Then the first few 2-highly polygonal numbers up to
, 4, ... up to some limit. Then the first few 2-highly polygonal numbers up to  are 1, 6, 9, 10, 12, 15, 16, 21, 28, (OEIS A090428). Similarly, the first few 3-highly polygonal numbers up to
are 1, 6, 9, 10, 12, 15, 16, 21, 28, (OEIS A090428). Similarly, the first few 3-highly polygonal numbers up to  are 1, 15, 36, 45, 325, 561, 1225, 1540, 3025, ... (OEIS A062712). There are no 4-highly polygonal numbers of this type less than
are 1, 15, 36, 45, 325, 561, 1225, 1540, 3025, ... (OEIS A062712). There are no 4-highly polygonal numbers of this type less than  except for 1.
except for 1.
The generating function for the 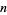 -gonal numbers is given by the beautiful formula
-gonal numbers is given by the beautiful formula
![G_n(x)=(x[(n-3)x+1])/((1-x)^3).](https://mathworld.wolfram.com/images/equations/PolygonalNumber/NumberedEquation4.gif) |
(6) |
Fermat proposed that every number is expressible as at most 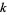
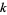 -gonal numbers (Fermat's polygonal number theorem). Fermat claimed to have a proof of this result, although this proof has never been found. Jacobi, Lagrange (in 1772), and Euler all proved the square case, and Gauss proved the triangular case in 1796. In 1813, Cauchy proved the proposition in its entirety.
-gonal numbers (Fermat's polygonal number theorem). Fermat claimed to have a proof of this result, although this proof has never been found. Jacobi, Lagrange (in 1772), and Euler all proved the square case, and Gauss proved the triangular case in 1796. In 1813, Cauchy proved the proposition in its entirety.
An arbitrary number 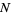 can be checked to see if it is a
can be checked to see if it is a 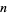 -gonal number as follows. Note the identity
-gonal number as follows. Note the identity
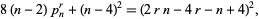 |
(7) |
so 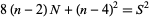 must be a perfect square. Therefore, if it is not, the number cannot be
must be a perfect square. Therefore, if it is not, the number cannot be 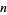 -gonal. If it is a perfect square, then solving
-gonal. If it is a perfect square, then solving
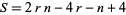 |
(8) |
for the rank 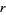 gives
gives
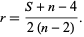 |
(9) |
An 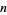 -gonal number is equal to the sum of the
-gonal number is equal to the sum of the 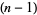 -gonal number of the same statistical rank and the triangular number of the previous statistical rank.
-gonal number of the same statistical rank and the triangular number of the previous statistical rank.
REFERENCES:
Abramovich, S.; Fujii, T.; and Wilson, J. W. "Multiple-Application Medium for the Study of Polygonal Numbers." https://jwilson.coe.uga.edu/Texts.Folder/AFW/AFWarticle.html.
Beiler, A. H. "Ball Games." Ch. 18 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, pp. 184-199, 1966.
Cauchy, A. "Démonstration du théorème général de Fermat sur les nombres polygones." Oeuvres, 2e. serie, Vol. 6. pp. 320-353.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 3-33, 2005.
Guy, K. "Every Number is Expressible as a Sum of How Many Polygonal Numbers?" Amer. Math. Monthly 101, 169-172, 1994.
Nathanson, M. B. "Sums of Polygonal Numbers." In Analytic Number Theory and Diophantine Problems: Proceedings of a Conference at Oklahoma State University, 1984 (Ed. A. Adolphson et al. ). Boston, MA: Birkhäuser, pp. 305-316, 1987.
Pappas, T. "Triangular, Square & Pentagonal Numbers." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 214, 1989.
Savin, A. "Shape Numbers." Quantum 11, 14-18, 2000.
Sloane, N. J. A. Sequences A000217/M2535, A062712, and A090428 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. Figure M2535 in The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|