


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-7-2020
Date: 12-1-2020
Date: 20-1-2020
|
Let the multiples 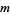 ,
, 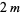 , ...,
, ..., ![[(p-1)/2]m](https://mathworld.wolfram.com/images/equations/GausssLemma/Inline3.gif) of an integer such that
of an integer such that 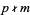 be taken. If there are an even number
be taken. If there are an even number 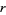 of least positive residues mod
of least positive residues mod 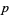 of these numbers
of these numbers 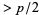 , then
, then 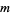 is a quadratic residue of
is a quadratic residue of 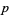 . If
. If 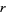 is odd,
is odd, 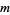 is a quadratic nonresidue. Gauss's lemma can therefore be stated as
is a quadratic nonresidue. Gauss's lemma can therefore be stated as 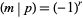 , where
, where 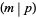 is the Legendre symbol. It was proved by Gauss as a step along the way to the quadratic reciprocity theorem (Nagell 1951).
is the Legendre symbol. It was proved by Gauss as a step along the way to the quadratic reciprocity theorem (Nagell 1951).
The following result is known as Euclid's lemma, but is incorrectly termed "Gauss's Lemma" by Séroul (2000, p. 10). Euclid's lemma states that for any two integers 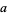 and
and 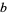 , suppose
, suppose 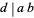 . Then if
. Then if 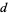 is relatively prime to
is relatively prime to 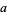 , then
, then 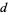 divides
divides 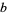 .
.
REFERENCES:
Nagell, T. "Gauss's Lemma." §40 in Introduction to Number Theory. New York: Wiley, pp. 139-141, 1951.
Séroul, R. "Gauss's Lemma." §2.4.2 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 10-11, 2000.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|