
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-1-2020
Date: 7-1-2021
Date: 22-12-2020
|
In April 1999, Ed Pegg conjectured on sci.math that there were only finitely many zerofree cubes, to which D. Hickerson responded with a counterexample. A few days later, Lew Baxter posted the slightly simpler example
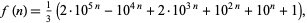 |
which produces numbers whose cubes lack zeros. The first few terms for 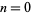 , 1, ... are 2, 64037, 6634003367, 666334000333667, ... (OEIS A052427). Primes occur for
, 1, ... are 2, 64037, 6634003367, 666334000333667, ... (OEIS A052427). Primes occur for 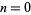 , 1, 7, 133, ... (OEIS A051832) with no others
, 1, 7, 133, ... (OEIS A051832) with no others 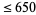 (Weisstein, pers. comm., 2002), corresponding to 2, 64037, 66666663333334000000033333336666667, ... (OEIS A051833).
(Weisstein, pers. comm., 2002), corresponding to 2, 64037, 66666663333334000000033333336666667, ... (OEIS A051833).
REFERENCES:
Pegg, E. Jr. "Fun with Numbers." http://www.mathpuzzle.com/numbers.html.
Sloane, N. J. A. Sequences A051832, A051833, and A052427 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|