


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-7-2020
Date: 14-12-2019
Date: 1-12-2020
|
 |
(1) |
Losanitsch's triangle (OEIS A034851) is a number triangle for which each term is the sum of the two numbers immediately above it, except that, numbering the rows by 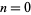 , 1, 2, ... and the entries in each row by
, 1, 2, ... and the entries in each row by 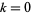 , 1, 2, ...,
, 1, 2, ..., 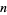 , are given by the recurrence equations
, are given by the recurrence equations
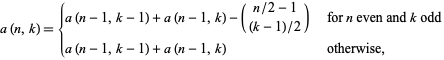 |
(2) |
where 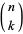 is a binomial coefficient.
is a binomial coefficient.
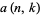 can be written in closed form as
can be written in closed form as
![a(n,k)=1/2[(n; k)+(n (mod 2); k (mod 2))(|_1/2n_|; |_1/2k_|)].](https://mathworld.wolfram.com/images/equations/LosanitschsTriangle/NumberedEquation3.gif) |
(3) |

The plot above shows the binary representations for the first 255 (top figure) and 511 (bottom figure) terms of a flattened Losanitsch's triangle.
The row sums of Losanitsch's triangle are
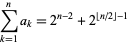 |
(4) |
the first few terms of which are 1, 2, 3, 6, 10, 20, 36, ... (OEIS A005418).
REFERENCES:
Losanitsch, S. M. "Die Isometrie-Arten bei den Homologen der Paraffin-Reihe." Chem. Ber. 30, 1917-1926, 1897.
Sloane, N. J. A. https://www.research.att.com/~njas/sequences/classic.html#LOSS.
Sloane, N. J. A. Sequences A005418 and A034851 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|