


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-8-2020
Date: 23-11-2019
Date: 23-2-2020
|
A general quadratic Diophantine equation in two variables  and
and 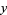 is given by
is given by
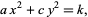 |
(1) |
where 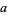 ,
, 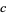 , and
, and 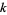 are specified (positive or negative) integers and
are specified (positive or negative) integers and  and
and 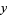 are unknown integers satisfying the equation whose values are sought. The slightly more general second-order equation
are unknown integers satisfying the equation whose values are sought. The slightly more general second-order equation
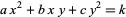 |
(2) |
is one of the principal topics in Gauss's Disquisitiones arithmeticae. According to Itô (1987), equation (2) can be solved completely using solutions to the Pell equation. In particular, all solutions of
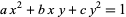 |
(3) |
are among the convergents of the continued fractions of the roots of 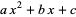 .
.
Solution to the general bivariate quadratic Diophantine equation is implemented in the Wolfram Language as Reduce[eqn && Element[x|y, Integers], 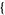 x, y
x, y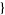 ].
].
For quadratic Diophantine equations in more than two variables, there exist additional deep results due to C. L. Siegel.
An equation of the form
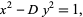 |
(4) |
where 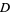 is an integer is a very special type of equation called a Pell equation. Pell equations, as well as the analogous equation with a minus sign on the right, can be solved by finding the continued fraction for
is an integer is a very special type of equation called a Pell equation. Pell equations, as well as the analogous equation with a minus sign on the right, can be solved by finding the continued fraction for 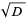 . The more complicated equation
. The more complicated equation
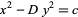 |
(5) |
can also be solved for certain values of 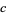 and
and 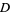 , but the procedure is more complicated (Chrystal 1961). However, if a single solution to (5) is known, other solutions can be found using the standard technique for the Pell equation.
, but the procedure is more complicated (Chrystal 1961). However, if a single solution to (5) is known, other solutions can be found using the standard technique for the Pell equation.
The following table summarizes possible representation of primes 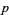 of given forms, where
of given forms, where  and
and 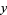 are positive integers. No odd primes other than those indicated share these properties (Nagell 1951, p. 188).
are positive integers. No odd primes other than those indicated share these properties (Nagell 1951, p. 188).
| form | congruence for 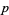 |
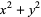 |
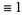 (mod 4) (mod 4) |
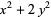 |
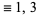 (mod 8) (mod 8) |
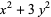 |
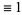 (mod 6) (mod 6) |
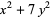 |
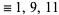 (mod 14) (mod 14) |
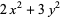 |
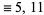 (mod 24) (mod 24) |
As a part of the study of Waring's problem, it is known that every positive integer is a sum of no more than 4 positive squares (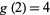 ; Lagrange's four-square theorem), that every "sufficiently large" integer is a sum of no more than 4 positive squares (
; Lagrange's four-square theorem), that every "sufficiently large" integer is a sum of no more than 4 positive squares (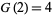 ), and that every integer is a sum of at most 3 signed squares (
), and that every integer is a sum of at most 3 signed squares (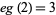 ). If zero is counted as a square, both positive and negative numbers are included, and the order of the two squares is distinguished, Jacobi showed that the number of ways a number can be written as the sum of two squares (the
). If zero is counted as a square, both positive and negative numbers are included, and the order of the two squares is distinguished, Jacobi showed that the number of ways a number can be written as the sum of two squares (the 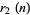 function) is four times the excess of the number of divisors of the form
function) is four times the excess of the number of divisors of the form 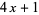 over the number of divisors of the form
over the number of divisors of the form 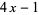 .
.
Given an initial solution 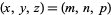 to the equation
to the equation
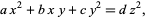 |
(6) |
a quadratic parametrization can be found using the identity
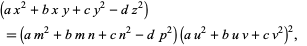 |
(7) |
where
 |
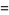 |
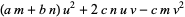 |
(8) |
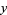 |
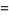 |
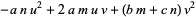 |
(9) |
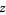 |
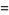 |
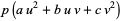 |
(10) |
for arbitrary 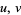 (T. Piezas, pers. comm., Apr. 28, 2006).
(T. Piezas, pers. comm., Apr. 28, 2006).
In 1769 Euler (1862) noted the identity
 |
(11) |
which gives a parametric solution to the equation
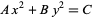 |
(12) |
for integers 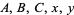 with
with 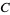 composite (Dickson 2005, p. 407).
composite (Dickson 2005, p. 407).
Call a Diophantine equation consisting of finding a sum of 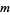
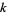 th powers which is equal to a sum of
th powers which is equal to a sum of 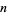
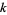 th powers a "
th powers a "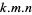 equation." The 2.1.2 quadratic Diophantine equation
equation." The 2.1.2 quadratic Diophantine equation
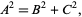 |
(13) |
corresponds to finding a Pythagorean triple (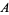 ,
, 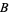 ,
, 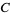 ) has a well-known general solution (Dickson 2005, pp. 165-170). To solve the equation, note that every prime of the form
) has a well-known general solution (Dickson 2005, pp. 165-170). To solve the equation, note that every prime of the form 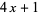 can be expressed as the sum of two relatively prime squares in exactly one way. A set of integers satisfying the 2.1.3 equation
can be expressed as the sum of two relatively prime squares in exactly one way. A set of integers satisfying the 2.1.3 equation
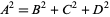 |
(14) |
is called a Pythagorean quadruple.
Parametric solutions to the 2.2.2 equation
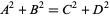 |
(15) |
are known (Dickson 2005; Guy 1994, p. 140). The number of solutions are given by the sum of squares function 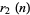 .
.
Solutions to an equation of the form
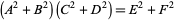 |
(16) |
are given by the Fibonacci identity
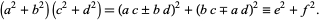 |
(17) |
Another similar identity is the Euler four-square identity
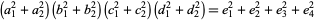 |
(18) |
 |
(19) |
Degen's eight-square identity holds for eight squares, but no other number, as proved by Cayley. The two-square identity underlies much of trigonometry, the four-square identity some of quaternions, and the eight-square identity, the Cayley algebra (a noncommutative nonassociative algebra; Bell 1945).
Chen Shuwen found the 2.6.6 equation
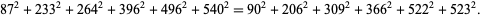 |
(20) |
Ramanujan's square equation
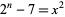 |
(21) |
has been proved to have only solutions 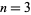 , 4, 5, 7, and 15 (Schroeppel 1972; OEIS A060728). In an unpublished proof, Euler showed that the quadratic Diophantine equation
, 4, 5, 7, and 15 (Schroeppel 1972; OEIS A060728). In an unpublished proof, Euler showed that the quadratic Diophantine equation
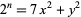 |
(22) |
has a unique solution for every positive 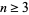 in which
in which  and
and 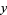 are both odd and positive (Engel 1998, p. 126). Rather amazingly, these can be given analytically by
are both odd and positive (Engel 1998, p. 126). Rather amazingly, these can be given analytically by
 |
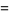 |
![(2^(n/2))/(sqrt(7))|sin[ntan^(-1)(sqrt(7))]|](https://mathworld.wolfram.com/images/equations/DiophantineEquation2ndPowers/Inline64.gif) |
(23) |
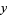 |
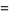 |
![2^(n/2)|cos[ntan^(-1)(sqrt(7))]|,](https://mathworld.wolfram.com/images/equations/DiophantineEquation2ndPowers/Inline67.gif) |
(24) |
which is related to the norms of elements of the ring of integers in the quadratic field 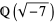 which exhibits unique factorization (Hickerson 2002). The first few solutions
which exhibits unique factorization (Hickerson 2002). The first few solutions 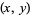 for
for 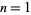 , 2, 3, ... are (1, 1), (1, 3), (1, 5), (3, 1), (1, 11), (5, 9), (7, 13), (3, 31), ... (OEIS A077020 and A077021).
, 2, 3, ... are (1, 1), (1, 3), (1, 5), (3, 1), (1, 11), (5, 9), (7, 13), (3, 31), ... (OEIS A077020 and A077021).
REFERENCES:
Beiler, A. H. "The Pellian." Ch. 22 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, pp. 248-268, 1966.
Bell, E. T. The Development of Mathematics, 2nd ed. New York: McGraw-Hill, p. 159, 1945.
Chrystal, G. Textbook of Algebra, 2 vols. New York: Chelsea, 1961.
Degan, C. F. Canon Pellianus. Copenhagen, Denmark, 1817.
Dickson, L. E. "Number of Representations as a Sum of 5, 6, 7, or 8 Squares." Ch. 13 in Studies in the Theory of Numbers. Chicago, IL: University of Chicago Press, 1930.
Dickson, L. E. "Pell Equation; 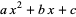 Made a Square" and "Further Single Equations of the Second Degree." Chs. 12-13 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 341-434, 2005.
Made a Square" and "Further Single Equations of the Second Degree." Chs. 12-13 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 341-434, 2005.
Engel, A. Problem-Solving Strategies. New York: Springer-Verlag, 1998.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.
Hickerson, D. "Re: Diophantine sequence" seqfan@ext.jussieu.fr mailing list. 17 Oct 2002.
Itô, K. (Ed.). Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 1. Cambridge, MA: MIT Press, p. 450, 1987.
Lam, T. Y. The Algebraic Theory of Quadratic Forms. Reading, MA: W. A. Benjamin, 1973.
Nagell, T. "Diophantine Equations of the Second Degree." Ch. 6 in Introduction to Number Theory. New York: Wiley, pp. 188-226, 1951.
Rajwade, A. R. Squares. Cambridge, England: Cambridge University Press, 1993.
Scharlau, W. Quadratic and Hermitian Forms. Berlin: Springer-Verlag, 1985.
Schroeppel, R. Item 31 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 14, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item31.
Shapiro, D. B. "Products of Sums and Squares." Expo. Math. 2, 235-261, 1984.
Sloane, N. J. A. Sequences A060728, A077020, and A077021 in "The On-Line Encyclopedia of Integer Sequences."
Smarandache, F. "Un metodo de resolucion de la ecuacion diofantica." Gaz. Math. 1, 151-157, 1988.
Smarandache, F. "Method to Solve the Diophantine Equation 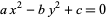 ." In Collected Papers, Vol. 1. Bucharest, Romania: Tempus, 1996.
." In Collected Papers, Vol. 1. Bucharest, Romania: Tempus, 1996.
Taussky, O. "Sums of Squares." Amer. Math. Monthly 77, 805-830, 1970.
Whitford, E. E. The Pell Equation. New York: Columbia University Press, 1912.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|