Lengyel's Constant

Let 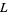 denote the partition lattice of the set . The maximum element of 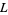 is

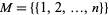(1)

and the minimum element is

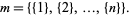(2)

Let 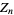 denote the number of chains of any length in  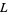containing both  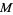and 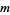. Then  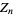satisfies the recurrence relation

(3)

where 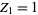 and 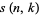 is a Stirling number of the second kind. The first few values of  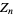for 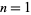, 2, ... are then 1, 1, 4, 32, 436, 9012, 262760, ... (OEIS A005121).

Lengyel (1984) proved that the quotient

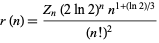(4)

is bounded between two constants as 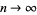, and Flajolet and Salvy (1990) improved the result of Babai and Lengyel (1992) to show that

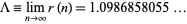(5)

(OEIS A086053).

REFERENCES:

Babai, L. and Lengyel, T. "A Convergence Criterion for Recurrent Sequences with Application to the Partition Lattice." Analysis 12, 109-119, 1992.

Finch, S. R. "Lengyel's Constant." §5.7 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 316-321, 2003.

Flajolet, P. and Salvy, B. "Hierarchal Set Partitions and Analytic Iterates of the Exponential Function." Unpublished manuscript, 1990.

Lengyel, T. "On a Recurrence Involving Stirling Numbers." Europ. J. Comb. 5, 313-321, 1984.

Sloane, N. J. A. Sequences A005121/M3649 and A086053 in "The On-Line Encyclopedia of Integer Sequences."