


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-7-2020
Date: 19-9-2020
Date: 26-1-2021
|
The number of cells in a generalized Chinese checkers board (or "centered" hexagram). Unlike the polygonal numbers, there is ambiguity in the case of the star numbers as to whether 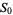 or
or 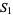 should be set equal to 1, since the equation defining star numbers never gives 0. For consistency with other figurate numbers, which are all defined such that
should be set equal to 1, since the equation defining star numbers never gives 0. For consistency with other figurate numbers, which are all defined such that 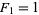 , that definition is used here as well, and
, that definition is used here as well, and 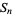 is defined by
is defined by
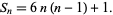 |
(1) |
The first few for 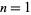 , 2, ... are 1, 13, 37, 73, 121, ... (OEIS A003154), and the generating function for the star numbers is
, 2, ... are 1, 13, 37, 73, 121, ... (OEIS A003154), and the generating function for the star numbers is
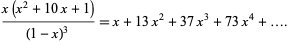 |
(2) |
The star numbers satisfy the linear recurrence equation
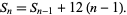 |
(3) |
Every star number has digital root 1 or 4, and the final digit must be one of 1, 3, or 7, and the final two digits must be one of 01, 13, 21, 33, 37, 41, 53, 61, 73, 81, or 93.
The first few triangular star numbers are 1, 253, 49141, 9533161, ... (OEIS A006060), and can be computed using
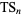 |
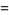 |
![(3[(7+4sqrt(3))^(2n-1)+(7-4sqrt(3))^(2n-1)]-10)/(32)](https://mathworld.wolfram.com/images/equations/StarNumber/Inline8.gif) |
(4) |
 |
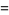 |
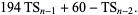 |
(5) |
The indices of the corresponding triangular numbers are 1, 22, 313, 4366, 60817, ... (OEIS A068774), and of the star numbers are 1, 7, 91, 1261, 17557, ... (OEIS A068775).
The first few square star numbers are 1, 121, 11881, 1164241, 114083761, ... (OEIS A006061). The indices of the corresponding square numbers are 1, 11, 109, 1079, 10681, 105731, 1046629, ... (OEIS A054320), and of the star numbers are 1, 5, 45, 441, 4361, 43165, 427285, ... (OEIS A068778). Square star numbers are obtained by solving the Diophantine equation
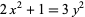 |
(6) |
and can be computed using
![SS_n=([(5+2sqrt(6))^n(sqrt(6)-2)-(5-2sqrt(6))^n(sqrt(6)+2)]^2)/4.](https://mathworld.wolfram.com/images/equations/StarNumber/NumberedEquation5.gif) |
(7) |
REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 41, 1996.
Gardner, M. "Hexes and Stars." Ch. 2 in Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, pp. 15-24, 1988.
Hindin, H. "Stars, Hexes, Triangular Numbers, and Pythagorean Triples." J. Recr. Math. 16, 191-193, 1983-1984.
Sloane, N. J. A. Sequences A003154/M4893, A006060/M5425, A006061/M5385, A054320, A068774, A068775, and A068778 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|