


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-11-2018
Date: 17-11-2018
Date: 18-12-2018
|
Conjugation is the process of taking a complex conjugate of a complex number, complex matrix, etc., or of performing a conjugation move on a knot.
Conjugation also has a meaning in group theory. Let 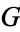 be a group and let
be a group and let 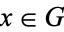 . Then,
. Then, 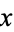 defines a homomorphism
defines a homomorphism 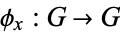 given by
given by
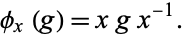 |
This is a homomorphism because
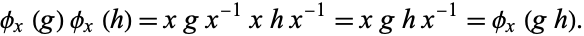 |
The operation on 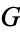 given by
given by 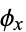 is called conjugation by
is called conjugation by 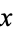 .
.
Conjugation is an important construction in group theory. Conjugation defines a group action of a group on itself and this often yields useful information about the group. For example, this technique is how the Sylow Theorems are proven. More importantly, a normal subgroup of a group is a subgroup which is invariant under conjugation by any element. Normal groups are extremely important because they are the kernels of homomorphisms and it is possible to take the quotient of a group and one of its normal subgroups.
REFERENCES:
Fraleigh, J. B. A First Course in Abstract Algebra, 7th ed. Reading, MA: Addison-Wesley, 2002.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|