Contour Winding Number

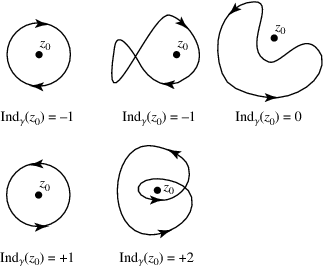
The winding number of a contour 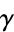 about a point 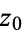, denoted 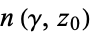, is defined by

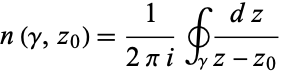and gives the number of times 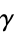 curve passes (counterclockwise) around a point. Counterclockwise winding is assigned a positive winding number, while clockwise winding is assigned a negative winding number. The winding number is also called the index, and denoted .

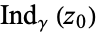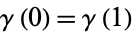The contour winding number was part of the inspiration for the idea of the Brouwer degree between two compact, oriented manifolds of the same dimension. In the language of the degree of a map, if  is a closed curve (i.e., ), then it can be considered as a function from  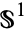to 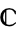. In that context, the winding number of 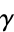around a point  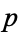in 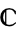 is given by the degree of the map

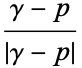from the circle to the circle.

REFERENCES:

Krantz, S. G. "The Index or Winding Number of a Curve about a Point." §4.4.4 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 49-50, 1999.