
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 5-8-2017
التاريخ: 6-8-2017
التاريخ: 8-8-2017
التاريخ: 6-8-2017
|
اسم الباحث: وسن شاكر جواد ناجي الطفيلي
الجامعه والكليه: كلية التربية في جامعة تكريت
الخلاصه :
لتكن R حلقة ابدالية ذات عنصر محايد وليكن M مقاساً ايسراً على R. يسمى M مقاساً اولياً اذا وفقط اذا كان 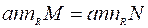 لكل مقاس جزئي غير صفري N من M. ليكن N مقاساً جزئياً فعلياً من المقاس M و N مقاساً جزئياً اولياً من M اذا كان
لكل مقاس جزئي غير صفري N من M. ليكن N مقاساً جزئياً فعلياً من المقاس M و N مقاساً جزئياً اولياً من M اذا كان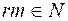 بحيث فإنه اما
بحيث فإنه اما 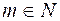 واما
واما 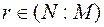 .
.
من المعروف اذا كان M مقاساً اولياً فإن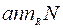 مثالي اولي في R لكل مقاس جزئي N من M لكن الاتجاه الاخر عبارة غير صادقة. هذه العبارة قادتنا الى تقديم المفهوم الاتي. يقال ان M مقاس اولي كاذب على الحلقة R اذا وفقط اذا كان
مثالي اولي في R لكل مقاس جزئي N من M لكن الاتجاه الاخر عبارة غير صادقة. هذه العبارة قادتنا الى تقديم المفهوم الاتي. يقال ان M مقاس اولي كاذب على الحلقة R اذا وفقط اذا كان مثالياً ابتدائياً(primary ideal )في R لكل مقاس جزئي غير صفري N من Mحيث يعرف المثالي الابتدائي في الحلقة R على انه اذا كان I حيث ان I a, b , اما I an واماI bk لبعض Z+n, k . نقدم في هذه الرسالة اعماماً للمقاس الاولي. يقال ان N مقاس جزئي كاذب من M اذا كان
مثالياً ابتدائياً(primary ideal )في R لكل مقاس جزئي غير صفري N من Mحيث يعرف المثالي الابتدائي في الحلقة R على انه اذا كان I حيث ان I a, b , اما I an واماI bk لبعض Z+n, k . نقدم في هذه الرسالة اعماماً للمقاس الاولي. يقال ان N مقاس جزئي كاذب من M اذا كان 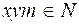 حيث
حيث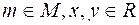 فإن اما
فإن اما 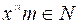 واما
واما 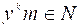 لبعض
لبعض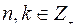 . ان هدفنا الرئيس في رسالتنا دراسة صفات المقاسات الاولية الكاذبة) pseudo prime R-modules)وصفات المقاسات الجزئية الاولية الكاذبة( pseudo prime submodules) ودراسة العلاقة بينهما.
. ان هدفنا الرئيس في رسالتنا دراسة صفات المقاسات الاولية الكاذبة) pseudo prime R-modules)وصفات المقاسات الجزئية الاولية الكاذبة( pseudo prime submodules) ودراسة العلاقة بينهما.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|