


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 6-3-2016
Date: 24-11-2020
Date: 13-9-2020
|
Work and Energy
Work is a very familiar concept! At a personal level it is the energy expended in carrying out a physical task. For example, work is done when a supermarket trolley is pushed along. Technically this work is defined simply as the product of the pushing force and the distance over which the trolley is pushed. (The standard unit of work and energy used in physics, called the joule, is the product of the unit of force (1N) multiplied by the unit of distance (lm).) Such a definition coincides readily with our perception of doing work the harder we push and/or the greater the distance covered, the greater the work done. Let us explore this example a little further. Consider first the very simple and ideal situation where there are no frictional forces acting and that the trolley is on a large plane surface. Starting from rest and exerting a constant force on the trolley means that it will move faster and faster it continually accelerates with an acceleration given by Newton’s Second Law. Suppose the trolley is pushed over a certain distance and then left to its own devices no friction and no pushing force. Since there are no forces acting on it, other than gravity holding it onto the ground, it will move along steadily in a straight line with whatever speed it reached whilst being accelerated by the pusher. The trolley clearly possesses energy by virtue of its motion. This is called kinetic energy and is exactly equal to the work that has been done by the pusher. It is proportional to the mass of the trolley and the square of its speed. More precisely, denoting the kinetic energy by E, for an object of mass m and speed v it is given by
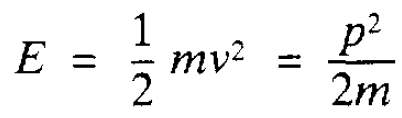
where (p = mv) is the magnitude of the body’s momentum. Intuitively one would expect kinetic energy to depend on these two quantities; the faster something moves and/or the more massive it is the more energy it will have. We have here a very simple example of another important conservation law the law of conservation of energy. The energy expended by the pusher in doing work is conserved as kinetic energy of the moving trolley. Consider now the more realistic situation when the trolley experiences friction as it is pushed along. As we to push the trolley along at a constant speed requires a steady force which balances the retarding force due to friction. Here the pusher is continually doing work and yet the kinetic. energy of the trolley is not increasing. So, if energy is conserved, where has the energy input from the pusher gone? The answer is that in overcoming the frictional force heat is generated-rub your hands together and you will at once feel such heat. Heat is another form of energy, as is evident from the working of steam engines, and the energy in the heat generated by friction is exactly equal to the energy expended by the pusher. Heat energy, is a form of internal kinetic energy associated with the motion of the atoms and molecules in a substance. Energy can take many forms. For example, imagine a car travelling along and suddenly having the brakes applied. Again there are frictional forces at work and, on application of the brakes, there is heating of the tyres and the road surface. There is also a screeching noise and the emitted sound carries away energy in the form of oscillations in the atmosphere. The effect of friction might be so large that sparks are emitted and then some energy is in the form of light. In this example the total energy in the heat, sound and light developed is equal to the kinetic energy of the car just before the brakes were applied. There is also another perspective on energy which it is important to understand. Suppose you lift a weight a certain distance upwards. The weight is stationary before and after it has been lifted and so at the end of the operation it has no kinetic energy. Yet work has been done and energy expended in lifting it. Where has that energy gone? The answer is that it has been stored. If the weight were allowed to fall back to its original position it would clearly then have kinetic energy and that kinetic energy would be found to be exactly equal to the work done against the force of gravity in lifting it from this position. In its raised position the weight has the potential to release energy (if it is allowed to fall) and this stored energy is referred to as potential energy. Potential energy is contained in a compressed spring, an extended elastic band, the fuel in a petrol tank, food, explosives and so on. So in considering the conservation of energy both kinetic energy (related to motion of some kind) and potential energy (stored energy) must both be taken into account. It should be stressed here that it is only meaningful to talk about potential and kinetic energy in a relative sense. In the foregoing example, the weight in its original position still has potential energy since it could be allowed to fall to an even lower position. The important quantity is the change in potential energy in moving between the original and the raised position. Similarly, with the supermarket trolley, the speed involved in specifying its kinetic energy is measured relative to the ground and if the study were conducted on a steadily moving walkway would be measured relative to the walkway. The law of conservation of energy in the form in which it. has been described holds with great accuracy for all everyday phenomena. However, the reader should be warned that when relativistic effects are taken into account, in particular the fact that mass itself can be converted into energy-witness the atomic bomb-then this conservation law has to be modified to take this convertibility into account and we finish up with the law of conservation of mass energy.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|