Hyper-P Algebra

Let 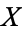 be a set of urelements that contains the set  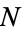of natural numbers, and let  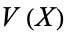be a superstructure whose individuals are in 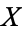. Let 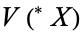 be an enlargement of 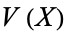, and let  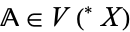be an algebra. Let  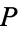be a property of algebras, expressed in the first-order language for the superstructure 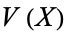. Then  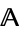is a hyper-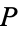-algebra provided that it satisfies  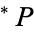in .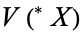

For example, let 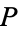 be the property of "being finite." Then  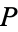is expressible in the first-order language for 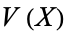, since 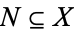, and a hyper- 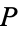algebra is just a hyperfinite algebra. One useful result involving hyperfinite algebras is the following: An algebra  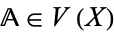is locally finite if and only if it has an hyperfinite extension in .

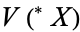For another example, consider the property of being a simple group. Then a hyper-simple group in 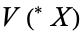 is just a group  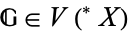which has exactly two internal normal subgroups, namely the trivial subgroup and the whole group 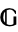. If an internal group is simple, then it is hyper-simple. It is not known if every hyper-simple group is simple.

For any property 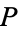, the following are equivalent:

1. 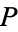 is finite generation-hereditary.

2. The following nonstandard characterization holds for 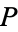: For any set  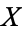of urelements, an algebra  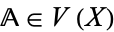is a local P-algebra if and only if  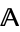has a hyper- 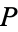extension in .

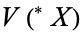REFERENCES:

Gehrke, M.; Kaiser, K.; and Insall, M. "Some Nonstandard Methods Applied to Distributive Lattices." Zeitschrifte für Mathematische Logik und Grundlagen der Mathematik 36, 123-131, 1990.

Insall, M. "Nonstandard Methods and Finiteness Conditions in Algebra." Zeitschr. f. Math., Logik, und Grundlagen d. Math. 37, 525-532, 1991.

Insall, M. "Some Finiteness Conditions in Lattices Using Nonstandard Proof Methods." J. Austral. Math. Soc. 53, 266-280, 1992.