Cardinal Addition

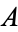Let  and 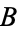 be any sets with empty intersection, and let  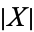denote the cardinal number of a set 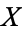. Then

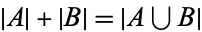(Ciesielski 1997, p. 68; Dauben 1990, p. 173; Rubin 1967, p. 274; Suppes 1972, pp. 112-113).

It is an interesting exercise to show that cardinal addition is well-defined. The main steps are to show that for any cardinal numbers 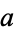 and 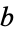, there exist disjoint sets  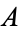and 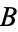 with cardinal numbers  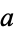and 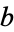, and to show that if  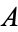and 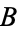 are disjoint 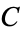and  and 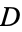 disjoint with  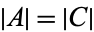and 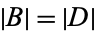 then 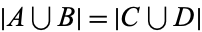. The second of these is easy. The first is a little tricky and requires an appeal to the axioms of set theory. Also, one needs to restrict the definition of cardinal to guarantee if  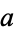is a cardinal, then there is a set  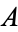satisfying .

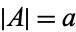REFERENCES:

Ciesielski, K. Set Theory for the Working Mathematician. Cambridge, England: Cambridge University Press, 1997.

Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1990.

Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.

Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.