Pitchfork Bifurcation

Let 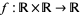 be a one-parameter family of  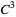maps satisfying

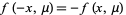	(1)
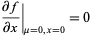	(2)
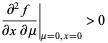	(3)
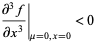	(4)

(Rasband 1990, p. 31), although condition (1) can actually be relaxed slightly. Then there are intervals having a single stable fixed point and three fixed points (two of which are stable and one of which is unstable). This type of bifurcation is called a pitchfork bifurcation.

An example of an equation displaying a pitchfork bifurcation is

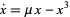(5)

(Guckenheimer and Holmes 1997, p. 145).

REFERENCES:

Guckenheimer, J. and Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, 3rd ed. New York: Springer-Verlag, pp. 145 and 149-150, 1997.

Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, p. 31, 1990.