


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-9-2021
Date: 17-11-2021
Date: 18-11-2021
|
An Anosov diffeomorphism is a 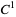 diffeomorphism
diffeomorphism 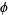 of a manifold
of a manifold 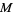 to itself such that the tangent bundle of
to itself such that the tangent bundle of 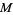 is hyperbolic with respect to
is hyperbolic with respect to 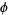 . Very few classes of Anosov diffeomorphisms are known. The best known is Arnold's cat map.
. Very few classes of Anosov diffeomorphisms are known. The best known is Arnold's cat map.
A hyperbolic linear map 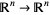 with integer entries in the transformation matrix and determinant
with integer entries in the transformation matrix and determinant 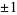 is an Anosov diffeomorphism of the
is an Anosov diffeomorphism of the 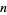 -torus. Not every manifold admits an Anosov diffeomorphism. Anosov diffeomorphisms are expansive, and there are no Anosov diffeomorphisms on the circle.
-torus. Not every manifold admits an Anosov diffeomorphism. Anosov diffeomorphisms are expansive, and there are no Anosov diffeomorphisms on the circle.
It is conjectured that if 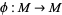 is an Anosov diffeomorphism on a compact Riemannian manifold and the nonwandering set
is an Anosov diffeomorphism on a compact Riemannian manifold and the nonwandering set 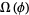 of
of 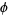 is
is 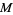 , then
, then 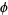 is topologically conjugate to a finite-to-one factor of an Anosov automorphism of a nilmanifold. It has been proved that any Anosov diffeomorphism on the
is topologically conjugate to a finite-to-one factor of an Anosov automorphism of a nilmanifold. It has been proved that any Anosov diffeomorphism on the 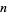 -torus is topologically conjugate to an Anosov automorphism, and also that Anosov diffeomorphisms are
-torus is topologically conjugate to an Anosov automorphism, and also that Anosov diffeomorphisms are 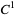 structurally stable.
structurally stable.
REFERENCES:
Anosov, D. V. "Geodesic Flow on Closed Riemannian Manifolds of Negative Curvature." Trudy Mat. Inst. Steklov 90, 1-209, 1970.
Smale, S. "Differentiable Dynamical Systems." Bull. Amer. Math. Soc. 73, 747-817, 1967.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|