


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-6-2021
Date: 22-7-2021
Date: 6-6-2021
|

The Perko pair is the pair of knots 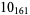 and
and 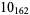 illustrated above. For many years, they were listed as separate knots in Little (1885) and all similar tables, including the pictorial enumeration of Rolfsen (1976, Appendix C). They were identified as identical by Perko (1974), who found that they are related to one another by the so-called Perko move (Perko 1974, Hoste et al. 1998). Although these knots are equivalent, their diagrams have different writhes (Hoste et al. 1998).
illustrated above. For many years, they were listed as separate knots in Little (1885) and all similar tables, including the pictorial enumeration of Rolfsen (1976, Appendix C). They were identified as identical by Perko (1974), who found that they are related to one another by the so-called Perko move (Perko 1974, Hoste et al. 1998). Although these knots are equivalent, their diagrams have different writhes (Hoste et al. 1998).
REFERENCES:
Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First 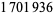 Knots." Math. Intell. 20, 33-48, Fall 1998.
Knots." Math. Intell. 20, 33-48, Fall 1998.
Little, C. N. "On Knots, with a Census of Order Ten." Trans. Connecticut Acad. Sci. 18, 374-378, 1885.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., p. 10, 1993.
Perko, K. A. Jr. "On the Classification of Knots." Proc. Amer. Math. Soc. 45, 262-266, 1974.
Rolfsen, D. "Table of Knots and Links." Appendix C in Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 280-287, 1976.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|