


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-8-2021
Date: 17-5-2021
Date: 20-6-2021
|
A hyperbolic knot is a knot that has a complement that can be given a metric of constant curvature 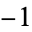 . All hyperbolic knots are prime knots (Hoste et al. 1998).
. All hyperbolic knots are prime knots (Hoste et al. 1998).

A prime knot on 10 or fewer crossings can be tested in the Wolfram Language to see if it is hyperbolic using KnotData[knot, "Hyperbolic"].
Of the prime knots with 16 or fewer crossings, all but 32 are hyperbolic. Of these 32, 12 are torus knots and the remaining 20 are satellites of the trefoil knot (Hoste et al. 1998). The nonhyperbolic knots with nine or fewer crossings are all torus knots, including 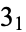 (the
(the 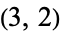 -torus knot),
-torus knot), 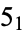 ,
, 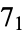 ,
, 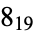 (the
(the 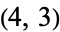 -torus knot), and
-torus knot), and 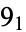 , the first few of which are illustrated above.
, the first few of which are illustrated above.
The following table gives the number of nonhyperbolic and hyperbolic knots of 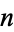 crossing starting with
crossing starting with 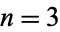 .
.
| type | OEIS | counts |
| torus | A051764 | 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 2, 1, ... |
| satellite | A051765 | 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 6, 10, ... |
| nonhyperbolic | A052407 | 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 3, 3, 8, 11, ... |
| hyperbolic | A052408 | 0, 1, 1, 3, 6, 20, 48, 164, 551, 2176, 9985, 46969, 253285, 1388694, ... |
Almost all hyperbolic knots can be distinguished by their hyperbolic volumes (exceptions being 05-002 and a certain 12-crossing knot; see Adams 1994, p. 124).
It was proved by Cao and Meyerhoff (2001) that the figure eight knot has the smallest possible hyperbolic volume, 2.0298.... The question of which knot has the second smallest hyperbolic volume remains open, but is conjectured to be 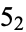 (which has the same hyperbolic volume as the 12-crossing knot mentioned above).
(which has the same hyperbolic volume as the 12-crossing knot mentioned above).
It has been conjectured that the smallest hyperbolic volume is 2.0298..., that of the figure eight knot.
Mutant knots have the same hyperbolic knot volume.
The knot symmetry group of a hyperbolic knot must be either a finite cyclic group or a finite dihedral group (Riley 1979, Kodama and Sakuma 1992, Hoste et al. 1998).
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 119-127, 1994.
Adams, C.; Hildebrand, M.; and Weeks, J. "Hyperbolic Invariants of Knots and Links." Trans. Amer. Math. Soc. 326, 1-56, 1991.
Cao, C. and Meyerhoff, G. R. "The Orientable Cusped Hyperbolic 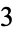 -Manifolds of Minimum Volume." Invent. Math. 146, 451-478, 2001.
-Manifolds of Minimum Volume." Invent. Math. 146, 451-478, 2001.
Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First 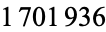 Knots." Math. Intell. 20, 33-48, Fall 1998.
Knots." Math. Intell. 20, 33-48, Fall 1998.
Kodama K. and Sakuma, M. "Symmetry Groups of Prime Knots Up to 10 Crossings." In Knot 90, Proceedings of the International Conference on Knot Theory and Related Topics, Osaka, Japan, 1990 (Ed. A. Kawauchi.) Berlin: de Gruyter, pp. 323-340, 1992.
Riley, R. "An Elliptic Path from Parabolic Representations to Hyperbolic Structures." In Topology of Low-Dimensional Manifolds, Proceedings, Sussex 1977 (Ed. R. Fenn). New York: Springer-Verlag, pp. 99-133, 1979.
Sloane, N. J. A. Sequences A051764, A051765, A052407, A052408 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|