Exponential Map

On a Lie group, exp is a map from the Lie algebra to its Lie group. If you think of the Lie algebra as the tangent space to the identity of the Lie group, exp(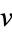) is defined to be 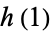, where  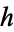is the unique Lie group homeomorphism from the real numbers to the Lie group such that its velocity at time 0 is .

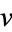On a Riemannian manifold, exp is a map from the tangent bundle of the manifold to the manifold, and exp(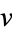) is defined to be 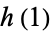, where  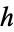is the unique geodesic traveling through the base-point of  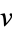such that its velocity at time 0 is .

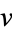The three notions of exp (exp from complex analysis, exp from Lie groups, and exp from Riemannian geometry) are all linked together, the strongest link being between the Lie groups and Riemannian geometry definition. If 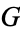 is a compact Lie group, it admits a left and right invariant Riemannian metric. With respect to that metric, the two exp maps agree on their common domain. In other words, one-parameter subgroups are geodesics. In the case of the manifold 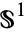, the circle, if we think of the tangent space to 1 as being the imaginary axis (y-axis) in the complex plane, then

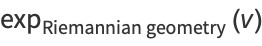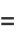			(1)
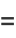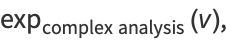			(2)

and so the three concepts of the exponential all agree in this case.

REFERENCES:

Huang, J.-S. "The Exponential Map." §7.3 in Lectures on Representation Theory. Singapore: World Scientific, p. v, 1999.