


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-10-2019
Date: 22-11-2019
Date: 4-1-2021
|
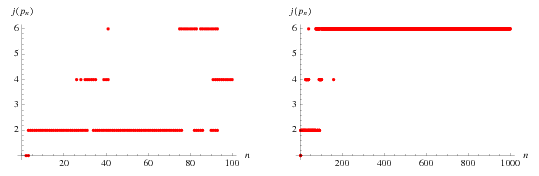
An integer 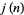 is called a jumping champion if
is called a jumping champion if 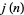 is the most frequently occurring difference between consecutive primes
is the most frequently occurring difference between consecutive primes 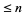 (Odlyzko et al. 1999). This term was coined by J. H. Conway in 1993. There are occasionally several jumping champions in a range. The scatter plots above show the jumping champions for small
(Odlyzko et al. 1999). This term was coined by J. H. Conway in 1993. There are occasionally several jumping champions in a range. The scatter plots above show the jumping champions for small 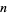 , and the ranges of number having given jumping champion sets are summarized in the following table.
, and the ranges of number having given jumping champion sets are summarized in the following table.
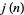 |
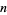 |
| 1 | 3 |
| 1, 2 | 5 |
| 2 | 7-100, 103-106, 109-112, ... |
| 2, 4 | 101-102, 107-108, 113-130, ... |
| 4 | 131-138, ... |
| 2, 4, 6 | 179-180, 467-490, ... |
| 2, 6 | 379-388, 421-432, ... |
| 6 | 389-420, ... |
Odlyzko et al. (1999) give a table of jumping champions for 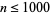 , consisting mainly of 2, 4, and 6. 6 is the jumping champion up to about
, consisting mainly of 2, 4, and 6. 6 is the jumping champion up to about 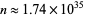 , at which point 30 dominates. At
, at which point 30 dominates. At 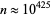 , 210 becomes champion, and subsequent primorials are conjectured to take over at larger and larger
, 210 becomes champion, and subsequent primorials are conjectured to take over at larger and larger 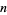 . Erdős and Straus (1980) proved that the jumping champions tend to infinity under the assumption of a quantitative form of the
. Erdős and Straus (1980) proved that the jumping champions tend to infinity under the assumption of a quantitative form of the 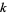 -tuples conjecture.
-tuples conjecture.
Wolf gives a table of approximate values 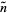 at which the primorial
at which the primorial 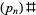 will become a champion. An estimate for
will become a champion. An estimate for 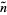 is given by
is given by
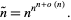 |
REFERENCES:
Erdős, P.; and Straus, E. G. "Remarks on the Differences Between Consecutive Primes." Elem. Math. 35, 115-118, 1980.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.
Nelson, H. "Problem 654." J. Recr. Math. 11, 231, 1978-1979.
Odlyzko, A.; Rubinstein, M.; and Wolf, M. "Jumping Champions." Experiment. Math. 8, 107-118, 1999.
Wolf, M. https://www.ift.uni.wroc.pl/~mwolf/.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|