


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-10-2019
Date: 22-4-2020
Date: 11-11-2019
|
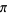 may be computed using a number of iterative algorithms. The best known such algorithms are the Archimedes algorithm, which was derived by Pfaff in 1800, and the Brent-Salamin formula. Borwein et al. (1989) discuss
may be computed using a number of iterative algorithms. The best known such algorithms are the Archimedes algorithm, which was derived by Pfaff in 1800, and the Brent-Salamin formula. Borwein et al. (1989) discuss 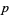 th-order iterative algorithms.
th-order iterative algorithms.
The Brent-Salamin formula is a quadratically converging algorithm.
Another quadratically converging algorithm (Borwein and Borwein 1987, pp. 46-48) is obtained by defining
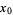 |
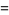 |
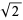 |
(1) |
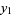 |
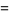 |
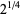 |
(2) |
and
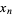 |
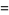 |
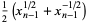 |
(3) |
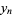 |
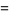 |
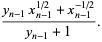 |
(4) |
Then
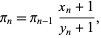 |
(5) |
with 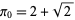 .
. 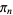 decreases monotonically to
decreases monotonically to 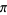 with
with
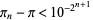 |
(6) |
for 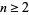 .
.
A cubically converging algorithm which converges to the nearest multiple of 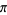 to
to 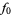 is the simple iteration
is the simple iteration
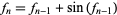 |
(7) |
(Beeler et al. 1972). For example, applying to 23 gives the sequence 23, 22.1537796, 21.99186453, 21.99114858, ..., which converges to 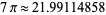 .
.
A quartically converging algorithm is obtained by letting
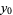 |
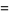 |
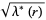 |
(8) |
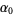 |
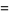 |
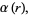 |
(9) |
then defining
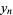 |
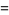 |
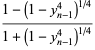 |
(10) |
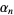 |
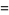 |
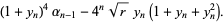 |
(11) |
Then
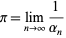 |
(12) |
and 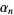 converges to
converges to 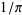 quartically with
quartically with
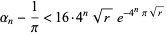 |
(13) |
(Borwein and Borwein 1987, pp. 170-171; Bailey 1988, Borwein et al. 1989). This algorithm rests on a modular equation identity of order 4. Taking the special case 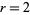 gives
gives 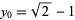 and
and 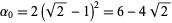 .
.
A quintically converging algorithm is obtained by letting
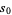 |
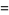 |
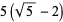 |
(14) |
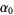 |
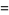 |
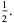 |
(15) |
Then let
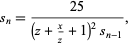 |
(16) |
where
 |
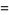 |
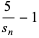 |
(17) |
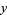 |
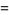 |
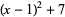 |
(18) |
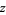 |
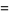 |
![[1/2x(y+sqrt(y^2-4x^3))]^(1/5).](https://mathworld.wolfram.com/images/equations/PiIterations/Inline53.gif) |
(19) |
Finally, let
![alpha_(n+1)=s_n^2alpha_n-5^n[1/2(s_n^2-5)+sqrt(s_n(s_n^2-2s_n+5))],](https://mathworld.wolfram.com/images/equations/PiIterations/NumberedEquation7.gif) |
(20) |
then
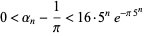 |
(21) |
(Borwein et al. 1989). This algorithm rests on a modular equation identity of order 5.
Beginning with any positive integer 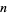 , round up to the nearest multiple of
, round up to the nearest multiple of 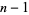 , then up to the nearest multiple of
, then up to the nearest multiple of 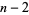 , and so on, up to the nearest multiple of 1. Let
, and so on, up to the nearest multiple of 1. Let 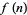 denote the result. Then the ratio
denote the result. Then the ratio
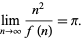 |
(22) |
David (1957) credits this result to Jabotinski and Erdős and gives the more precise asymptotic result
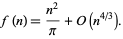 |
(23) |
The first few numbers in the sequence  are 1, 2, 4, 6, 10, 12, 18, 22, 30, 34, ... (OEIS A002491).
are 1, 2, 4, 6, 10, 12, 18, 22, 30, 34, ... (OEIS A002491).
Another algorithm is due to Woon (1995). Define 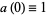 and
and
![a(n)=sqrt(1+[sum_(k=0)^(n-1)a(k)]^2).](https://mathworld.wolfram.com/images/equations/PiIterations/NumberedEquation11.gif) |
(24) |
It can be proved by induction that
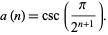 |
(25) |
For 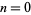 , the identity holds. If it holds for
, the identity holds. If it holds for 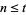 , then
, then
![a(t+1)=sqrt(1+[sum_(k=0)^tcsc(pi/(2^(k+1)))]^2),](https://mathworld.wolfram.com/images/equations/PiIterations/NumberedEquation13.gif) |
(26) |
but
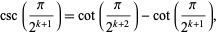 |
(27) |
so
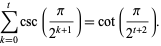 |
(28) |
Therefore,
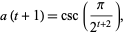 |
(29) |
so the identity holds for 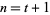 and, by induction, for all nonnegative
and, by induction, for all nonnegative 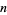 , and
, and
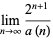 |
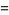 |
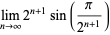 |
(30) |
 |
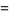 |
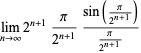 |
(31) |
 |
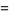 |
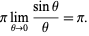 |
(32) |
REFERENCES:
Bailey, D. H. "The Computation of  to
to  Decimal Digit using Borwein's' Quartically Convergent Algorithm." Math. Comput. 50, 283-296, 1988.
Decimal Digit using Borwein's' Quartically Convergent Algorithm." Math. Comput. 50, 283-296, 1988.
Beeler, M. et al. Item 140 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 69, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/pi.html#item140.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "Ramanujan, Modular Equations, and Approximations to Pi, or How to Compute One Billion Digits of Pi." Amer. Math. Monthly 96, 201-219, 1989.
David, Y. "On a Sequence Generated by a Sieving Process." Riveon Lematematika 11, 26-31, 1957.
Sloane, N. J. A. Sequence A002491/M1009 in "The On-Line Encyclopedia of Integer Sequences."
Woon, S. C. "Problem 1441." Math. Mag. 68, 72-73, 1995.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|