


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-10-2020
Date: 25-12-2020
Date: 4-2-2020
|
A curious approximation to the Feigenbaum constant 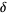 is given by
is given by
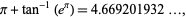 |
(1) |
where 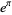 is Gelfond's constant, which is good to 6 digits to the right of the decimal point.
is Gelfond's constant, which is good to 6 digits to the right of the decimal point.
M. Trott (pers. comm., May 6, 2008) noted
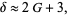 |
(2) |
where 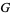 is Gauss's constant, which is good to 4 decimal digits, and
is Gauss's constant, which is good to 4 decimal digits, and
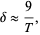 |
(3) |
where 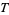 is the tetranacci constant, which is good to 3 decimal digits.
is the tetranacci constant, which is good to 3 decimal digits.
A strange approximation good to five digits is given by the solution to
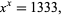 |
(4) |
which is
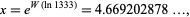 |
(5) |
where 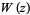 is the Lambert W-function (G. Deppe, pers. comm., Feb. 27, 2003).
is the Lambert W-function (G. Deppe, pers. comm., Feb. 27, 2003).
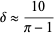 |
(6) |
gives 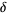 to 3 digits (S. Plouffe, pers. comm., Apr. 10, 2006).
to 3 digits (S. Plouffe, pers. comm., Apr. 10, 2006).
M. Hudson (pers. comm., Nov. 20, 2004) gave
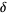 |
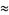 |
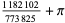 |
(7) |
 |
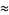 |
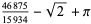 |
(8) |
 |
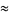 |
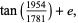 |
(9) |
which are good to 17, 13, and 9 digits respectively.
Stoschek gave the strange approximation
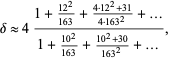 |
(10) |
which is good to 9 digits.
R. Phillips (pers. comm., Sept. 14, 2004-Jan. 25, 2005) gave the approximations
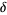 |
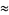 |
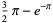 |
(11) |
 |
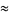 |
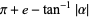 |
(12) |
 |
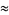 |
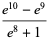 |
(13) |
 |
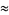 |
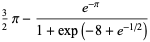 |
(14) |
 |
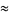 |
![pi-tan^(-1)[(e-1)^(-16)-e^pi],](http://mathworld.wolfram.com/images/equations/FeigenbaumConstantApproximations/Inline30.gif) |
(15) |
 |
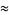 |
![(e(e-1))/(1+exp{8[(1+e^(-8))^(3/2)-2]})](http://mathworld.wolfram.com/images/equations/FeigenbaumConstantApproximations/Inline33.gif) |
(16) |
where e is the base of the natural logarithm and 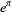 is Gelfond's constant, which are good to 3, 3, 5, 7, 9, and 10 decimal digits, respectively, and
is Gelfond's constant, which are good to 3, 3, 5, 7, 9, and 10 decimal digits, respectively, and
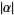 |
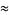 |
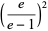 |
(17) |
 |
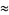 |
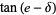 |
(18) |
 |
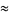 |
![tan[e-tan^(-1)(e^pi)]](http://mathworld.wolfram.com/images/equations/FeigenbaumConstantApproximations/Inline43.gif) |
(19) |
 |
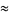 |
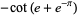 |
(20) |
 |
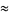 |
![tan[e+tan^(-1)(2/((e-1)^8e)-e^pi)]](http://mathworld.wolfram.com/images/equations/FeigenbaumConstantApproximations/Inline49.gif) |
(21) |
 |
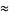 |
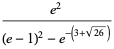 |
(22) |
 |
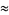 |
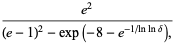 |
(23) |
which are good to 3, 3, 3, 4, 6, 8, and 8 decimal digits, respectively.
An approximation to 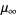 due to R. Phillips (pers. comm., Jan. 27, 2005) is obtained by numerically solving
due to R. Phillips (pers. comm., Jan. 27, 2005) is obtained by numerically solving
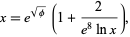 |
(24) |
for  , where
, where 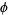 is the golden ratio, which is good to 4 digits.
is the golden ratio, which is good to 4 digits.
REFERENCES:
Friedman, E. "Problem of the Month (August 2004)." http://www.stetson.edu/~efriedma/mathmagic/0804.html.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|