Ball Line Picking

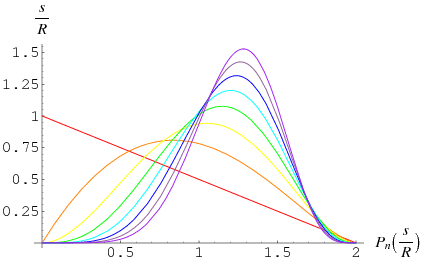
Given an 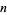-ball 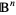 of radius 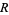, find the distribution of the lengths  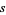of the lines determined by two points chosen at random within the ball. The probability distribution of lengths is given by

(1)

where

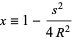(2)

and

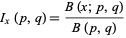(3)

is a regularized beta function, with 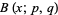 is an incomplete beta function and  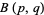is a beta function (Tu and Fischbach 2000).

The first few are

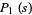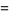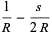			(4)
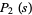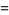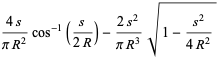			(5)
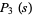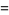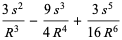			(6)
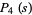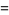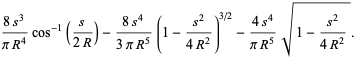			(7)

The mean line segment lengths for 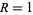 and the first few dimensions  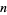are given by

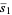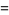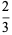			(8)
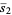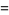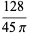			(9)
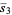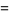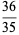			(10)
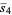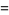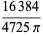			(11)

(OEIS A093530 and A093531 and OEIS A093532 and A093533), corresponding to line line picking, disk line picking, (3-D) ball line picking, and so on.

REFERENCES:

Kendall, M. G. and Moran, P. A. P. Geometrical Probability. New York: Hafner, 1963.

Santaló, L. A. Integral Geometry and Geometric Probability. Reading, MA: Addison-Wesley, 1976.

Sloane, N. J. A. Sequences A093530, A093531, A093532, and A093533 in "The On-Line Encyclopedia of Integer Sequences."

Tu, S.-J. and Fischbach, E. "A New Geometric Probability Technique for an 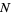-Dimensional Sphere and Its Applications" 17 Apr 2000. http://arxiv.org/abs/math-ph/0004021.