


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-8-2020
Date: 16-2-2020
Date: 16-7-2020
|
Catalan's constant is a constant that commonly appears in estimates of combinatorial functions and in certain classes of sums and definite integrals. It is usually denoted 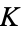 (this work),
(this work), 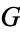 (e.g., Borwein et al. 2004, p. 49), or
(e.g., Borwein et al. 2004, p. 49), or 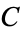 (Wolfram Language).
(Wolfram Language).
Catalan's constant may be defined by
 |
(1) |
(Glaisher 1877, who however did not explicitly identify the constant in this paper). It is not known if 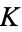 is irrational.
is irrational.
Catalan's constant is implemented in the Wolfram Language as Catalan.
The constant is named in honor of E. C. Catalan (1814-1894), who first gave an equivalent series and expressions in terms of integrals. Numerically,
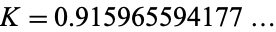 |
(2) |
(OEIS A006752).
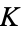 can be given analytically by the following expressions
can be given analytically by the following expressions
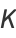 |
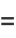 |
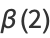 |
(3) |
 |
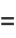 |
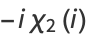 |
(4) |
 |
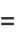 |
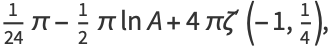 |
(5) |
where 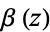 is the Dirichlet beta function,
is the Dirichlet beta function, 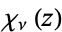 is Legendre's chi-function,
is Legendre's chi-function, 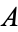 is the Glaisher-Kinkelin constant, and
is the Glaisher-Kinkelin constant, and 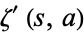 is the partial derivative of the Hurwitz zeta function with respect to the first argument.
is the partial derivative of the Hurwitz zeta function with respect to the first argument.
Glaisher (1913) gave
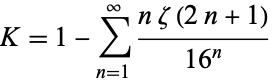 |
(6) |
(Vardi 1991, p. 159). It is also given by the sums
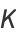 |
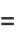 |
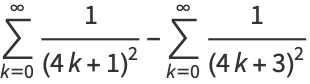 |
(7) |
 |
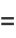 |
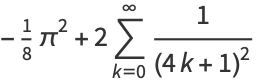 |
(8) |
 |
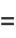 |
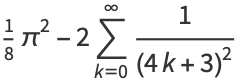 |
(9) |
Equations (◇) and (◇) follow from
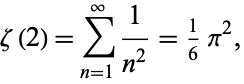 |
(10) |
together with
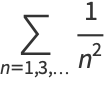 |
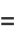 |
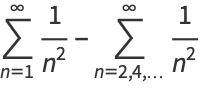 |
(11) |
 |
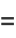 |
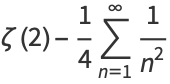 |
(12) |
 |
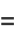 |
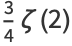 |
(13) |
 |
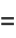 |
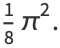 |
(14) |
But
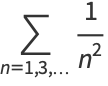 |
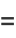 |
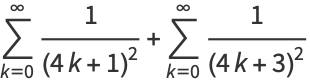 |
(15) |
 |
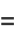 |
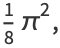 |
(16) |
so combining (16) with (◇) gives (◇) and (◇).
Applying convergence improvement to (◇) gives
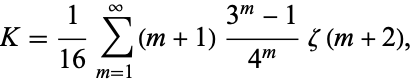 |
(17) |
where 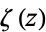 is the Riemann zeta function and the identity
is the Riemann zeta function and the identity
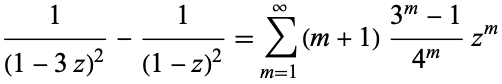 |
(18) |
has been used (Flajolet and Vardi 1996).
A beautiful double series due to O. Oloa (pers. comm., Dec. 30, 2005) is given by
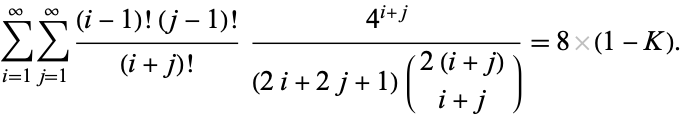 |
(19) |
There are a large number of BBP-type formulas with coefficient 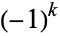 , the first few being
, the first few being
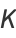 |
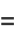 |
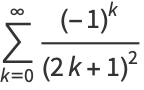 |
(20) |
 |
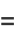 |
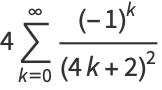 |
(21) |
 |
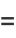 |
![sum_(k=0)^(infty)(-1)^k[1/((6k+1)^2)-1/((6k+3)^2)+1/((6k+5)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline56.gif) |
(22) |
 |
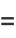 |
![1/3sum_(k=0)^(infty)(-1)^k[2/((6k+1)^2)+7/((6k+3)^2)+2/((6k+5)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline59.gif) |
(23) |
 |
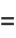 |
![sum_(k=0)^(infty)(-1)^k[1/((10k+1)^2)-1/((10k+3)^2)+1/((10k+5)^2)-1/((10k+7)^2)+1/((10k+9)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline62.gif) |
(24) |
 |
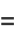 |
![1/3sum_(k=0)^(infty)(-1)^k[4/((10k+1)^2)-4/((10k+3)^2)-(21)/((10k+5)^2)-4/((10k+7)^2)+4/((10k+9)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline65.gif) |
(25) |
 |
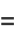 |
![sum_(k=0)^(infty)(-1)^k[1/((14k+1)^2)-1/((14k+3)^2)+1/((14k+5)^2)-1/((14k+7)^2)+1/((14k+9)^2)-1/((14k+11)^2)+1/((14k+13)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline68.gif) |
(26) |
 |
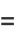 |
![1/6sum_(k=0)^(infty)(-1)^k[5/((14k+1)^2)-5/((14k+3)^2)+5/((14k+5)^2)+(44)/((14k+7)^2)+5/((14k+9)^2)-5/((14k+11)^2)+5/((14k+13)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline71.gif) |
(27) |
(E. W. Weisstein, Feb. 26, 2006).
BBP-type formula identities for 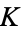 with higher powers include
with higher powers include
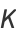 |
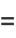 |
![3/(64)sum_(k=0)^(infty)((-1)^k)/(64^k)[(32)/((12k+1)^2)-(32)/((12k+2)^2)-(32)/((12k+3)^2)-8/((12k+5)^2)-(16)/((12k+6)^2)-4/((12k+7)^2)-4/((12k+9)^2)-2/((12k+10)^2)+1/((12k+11)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline75.gif) |
(28) |
(V. Adamchik, pers. comm., Sep. 28, 2007),
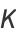 |
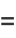 |
![5/(1024)sum_(k=0)^(infty)((-1)^k)/(1024^k)[(512)/((20k+1)^2)-(1536)/((20k+2)^2)+(256)/((20k+3)^2)+(512)/((20k+5)^2)+(384)/((20k+6)^2)-(64)/((20k+7)^2)+(32)/((20k+9)^2)+(64)/((20k+10)^2)+(64)/((20k+11)^2)+(16)/((20k+12)^2)-8/((20k+13)^2)+(24)/((20k+14)^2)+(16)/((20k+15)^2)+2/((20k+16)^2)+2/((20k+17)^2)-6/((20k+18)^2)+1/((20k+19)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline78.gif) |
(29) |
(E. W. Weisstein, Sep. 30, 2007),
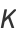 |
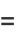 |
![1/(1024)sum_(k=0)^(infty)1/(4096^k)[(3072)/((24k+1)^2)-(3072)/((24k+2)^2)-(23040)/((24k+3)^2)+(12288)/((24k+4)^2)-(768)/((24k+5)^2)+(9216)/((24k+6)^2)+(10368)/((24k+8)^2)+(2496)/((24k+9)^2)-(192)/((24k+10)^2)+(768)/((24k+12)^2)-(48)/((24k+13)^2)+(360)/((24k+15)^2)+(648)/((24k+16)^2)+(12)/((24k+17)^2)+(168)/((24k+18)^2)+(48)/((24k+20)^2)-(39)/((24k+21)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline81.gif) |
(30) |
(Borwein and Bailey 2003, p. 128), and
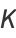 |
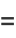 |
![1/(1024)sum_(k=0)^(infty)1/(4096^k)[(1024)/((24k+1)^2)+(1024)/((24k+2)^2)-(512)/((24k+3)^2)-(3072)/((24k+4)^2)-(256)/((24k+5)^2)-(2048)/((24k+6)^2)-(256)/((24k+7)^2)-(1152)/((24k+8)^2)-(320)/((24k+9)^2)+(64)/((24k+10)^2)+(64)/((24k+11)^2)-(16)/((24k+13)^2)+(64)/((24k+14)^2)+8/((24k+15)^2)-(72)/((24k+16)^2)+4/((24k+17)^2)-8/((24k+18)^2)+4/((24k+19)^2)-(12)/((24k+20)^2)+5/((24k+21)^2)+4/((24k+22)^2)-1/((24k+23)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline84.gif) |
(31) |
 |
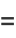 |
![1/(3072)sum_(k=0)^(infty)1/(4096^k)[(5120)/((24k+1)^2)-(8192)/((24k+2)^2)-(2560)/((24k+3)^2)+(2560)/((24k+4)^2)-(1280)/((24k+5)^2)-(2048)/((24k+6)^2)-(512)/((24k+7)^2)-(832)/((24k+9)^2)-(512)/((24k+10)^2)+(128)/((24k+11)^2)-(128)/((24k+12)^2)-(80)/((24k+13)^2)+(16)/((24k+14)^2)+(40)/((24k+15)^2)+(20)/((24k+17)^2)+(40)/((24k+18)^2)+8/((24k+19)^2)+(10)/((24k+20)^2)+(13)/((24k+21)^2)+1/((24k+22)^2)-2/((24k+23)^2)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline87.gif) |
(32) |
(E. W. Weisstein, Feb. 25, 2006).
A rapidly converging Zeilberger-type sum due to A. Lupas is given by
![K=1/(64)sum_(n=1)^infty((-1)^(n-1)2^(8n)(40n^2-24n+3)[(2n)!]^3(n!)^2)/(n^3(2n-1)[(4n)!]^2)](http://mathworld.wolfram.com/images/equations/CatalansConstant/NumberedEquation8.gif) |
(33) |
(Lupas 2000), and is used to calculate 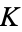 in the Wolfram Language.
in the Wolfram Language.
Catalan's constant is also given by the integrals
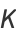 |
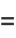 |
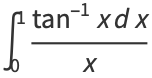 |
(34) |
 |
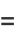 |
![int_0^13/xtan^(-1)[(x(1-x))/(2-x)]dx](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline94.gif) |
(35) |
 |
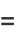 |
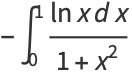 |
(36) |
 |
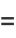 |
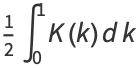 |
(37) |
 |
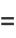 |
![-int_0^(pi/2)ln[2sin(1/2t)]dt](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline103.gif) |
(38) |
 |
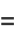 |
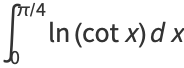 |
(39) |
 |
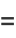 |
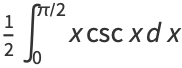 |
(40) |
 |
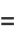 |
 |
(41) |
 |
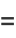 |
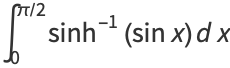 |
(42) |
 |
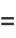 |
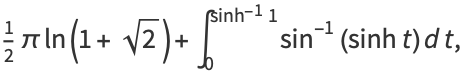 |
(43) |
where (37) is from Mc Laughlin (2007; which corresponds to the 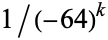 BBP-type formula), (38) is from Borwein et al. (2004, p. 106), (40) is from Glaisher (1877), (41) is from J. Borwein (pers. comm., Jul. 16, 2007), (42) is from Adamchik, and (43) is from W. Gosper (pers. comm., Jun. 11, 2008). Here,
BBP-type formula), (38) is from Borwein et al. (2004, p. 106), (40) is from Glaisher (1877), (41) is from J. Borwein (pers. comm., Jul. 16, 2007), (42) is from Adamchik, and (43) is from W. Gosper (pers. comm., Jun. 11, 2008). Here, 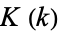 (not to be confused with Catalan's constant itself) is a complete elliptic integral of the first kind. Zudilin (2003) gives the unit square integral
(not to be confused with Catalan's constant itself) is a complete elliptic integral of the first kind. Zudilin (2003) gives the unit square integral
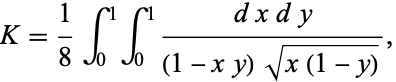 |
(44) |
which is the analog of a double integral for 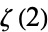 due to Beukers (1979).
due to Beukers (1979).
In terms of the trigamma function 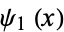 ,
,
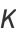 |
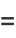 |
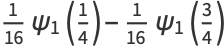 |
(45) |
 |
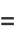 |
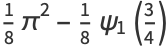 |
(46) |
 |
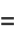 |
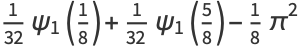 |
(47) |
 |
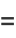 |
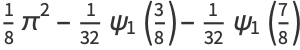 |
(48) |
 |
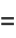 |
![1/(64)[psi_1(1/8)-psi_1(3/8)+psi_1(5/8)-psi_1(7/8)]](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline137.gif) |
(49) |
 |
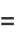 |
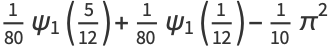 |
(50) |
 |
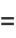 |
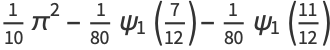 |
(51) |
 |
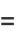 |
![1/(160)[psi_1(1/(12))+psi_1(5/(12))-psi_1(7/(12))-psi_1((11)/(12))].](http://mathworld.wolfram.com/images/equations/CatalansConstant/Inline146.gif) |
(52) |
Catalan's constant also arises in products, such as
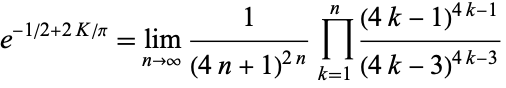 |
(53) |
(Glaisher 1877).
Zudilin (2003) gives the continued fraction
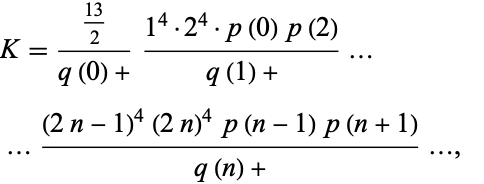 |
(54) |
where
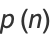 |
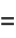 |
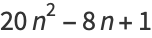 |
(55) |
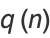 |
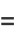 |
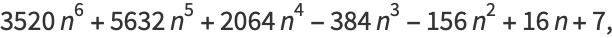 |
(56) |
which is an analog of the continued fraction of Apéry's constant found by Apéry (1979).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 807-808, 1972.
Adamchik, V. "Integral and Series Representations for Catalan's Constant." http://www-2.cs.cmu.edu/~adamchik/articles/catalan.htm.
Adamchik, V. "Thirty-Three Representations of Catalan's Constant." http://library.wolfram.com/infocenter/Demos/109/.
Apéry, R. "Irrationalité de 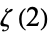 et
et 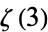 ." Astérisque 61, 11-13, 1979.
." Astérisque 61, 11-13, 1979.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 551-552, 1985.
Beukers, F. "A Note on the Irrationality of 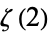 and
and 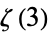 ." Bull. London Math. Soc. 11, 268-272, 1979.
." Bull. London Math. Soc. 11, 268-272, 1979.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Catalan, E. "Sur la transformation des series, et sur quelques integrales definies." Mémoires in 4 de l'Academie royale de Belgique, 1865.
Catalan, E. "Recherches sur la constant 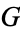 , et sur les integrales euleriennes." Mémoires de l'Academie imperiale des sciences de Saint-Pétersbourg, Ser. 7, 31, 1883.
, et sur les integrales euleriennes." Mémoires de l'Academie imperiale des sciences de Saint-Pétersbourg, Ser. 7, 31, 1883.
Fee, G. J. "Computation of Catalan's Constant using Ramanujan's Formula." ISAAC '90. Proc. Internat. Symp. Symbolic Algebraic Comp., Aug. 1990. Reading, MA: Addison-Wesley, 1990.
Finch, S. R. "Catalan's Constant." §1.7 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 53-59, 2003.
Flajolet, P. and Vardi, I. "Zeta Function Expansions of Classical Constants." Unpublished manuscript. 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.
Glaisher, J. W. L. "On a Numerical Continued Product." Messenger Math. 6, 71-76, 1877.
Gosper, R. W. "A Calculus of Series Rearrangements." In Algorithms and Complexity: New Directions and Recent Results. Proc. 1976 Carnegie-Mellon Conference (Ed. J. F. Traub). New York: Academic Press, pp. 121-151, 1976.
Gosper, R. W. "Thought for Today." math-fun@cs.arizona.edu posting, Aug. 8, 1996.
Lupas, A. "Formulae for Some Classical Constants." In Proceedings of ROGER-2000. 2000. http://www.lacim.uqam.ca/~plouffe/articles/alupas1.pdf.
Mc Laughlin, J. "An Integral for Catalan's Constant." 27 Sep 2007. http://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0709&L=nmbrthry&T=0&P=3444.
Nielsen, N. Der Eulersche Dilogarithms. Leipzig, Germany: Halle, pp. 105 and 151, 1909.
Plouffe, S. "Table of Current Records for the Computation of Constants." http://pi.lacim.uqam.ca/eng/records_en.html.
Rivoal, T. and Zudilin, W. "Diophantine Properties of Numbers Related to Catalan's Constant." Math. Ann. 326, 705-721, 2003. http://www.mi.uni-koeln.de/~wzudilin/beta.pdf.
Sloane, N. J. A. Sequence A006752/M4593 in "The On-Line Encyclopedia of Integer Sequences."
Srivastava, H. M. and Miller, E. A. "A Simple Reducible Case of Double Hypergeometric Series involving Catalan's Constant and Riemann's Zeta Function." Int. J. Math. Educ. Sci. Technol. 21, 375-377, 1990.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 159, 1991.
Yang, S. "Some Properties of Catalan's Constant 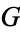 ." Int. J. Math. Educ. Sci. Technol. 23, 549-556, 1992.
." Int. J. Math. Educ. Sci. Technol. 23, 549-556, 1992.
Zudilin, W. "An Apéry-Like Difference Equation for Catalan's Constant." Electronic J. Combinatorics 10, No. 1, R14, 1-10, 2003. http://www.combinatorics.org/Volume_10/Abstracts/v10i1r14.html.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|