


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-8-2020
Date: 21-12-2019
Date: 18-4-2020
|
In his monumental treatise Disquisitiones Arithmeticae, Gauss conjectured that the class number 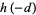 of an imaginary quadratic field with binary quadratic form discriminant
of an imaginary quadratic field with binary quadratic form discriminant 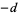 tends to infinity with
tends to infinity with 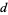 . A proof was finally given by Heilbronn (1934), and Siegel (1936) showed that for any
. A proof was finally given by Heilbronn (1934), and Siegel (1936) showed that for any 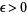 , there exists a constant
, there exists a constant 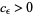 such that
such that
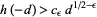 |
as 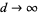 . However, these results were not effective in actually determining the values for a given
. However, these results were not effective in actually determining the values for a given 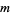 of a complete list of fundamental discriminants
of a complete list of fundamental discriminants  such that
such that 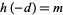 , a problem known as Gauss's class number problem.
, a problem known as Gauss's class number problem.
Goldfeld (1976) showed that if there exists a "Weil curve" whose associated Dirichlet L-series has a zero of at least third order at 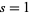 , then for any
, then for any 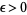 , there exists an effectively computable constant
, there exists an effectively computable constant 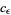 such that
such that
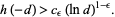 |
Gross and Zaiger (1983) showed that certain curves must satisfy the condition of Goldfeld, and Goldfeld's proof was simplified by Oesterlé (1985).
REFERENCES:
Arno, S.; Robinson, M. L.; and Wheeler, F. S. "Imaginary Quadratic Fields with Small Odd Class Number." http://www.math.uiuc.edu/Algebraic-Number-Theory/0009/.
Böcherer, S. "Das Gauß'sche Klassenzahlproblem." Mitt. Math. Ges. Hamburg 11, 565-589, 1988.
Gauss, C. F. Disquisitiones Arithmeticae. New Haven, CT: Yale University Press, 1966.
Goldfeld, D. M. "The Class Number of Quadratic Fields and the Conjectures of Birch and Swinnerton-Dyer." Ann. Scuola Norm. Sup. Pisa 3, 623-663, 1976.
Gross, B. and Zaiger, D. "Points de Heegner et derivées de fonctions 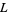 ." Comptes Rendus Acad. Sci. Paris 297, 85-87, 1983.
." Comptes Rendus Acad. Sci. Paris 297, 85-87, 1983.
Heilbronn, H. "On the Class Number in Imaginary Quadratic Fields." Quart. J. Math. Oxford Ser. 25, 150-160, 1934.
Oesterlé, J. "Nombres de classes des corps quadratiques imaginaires." Astérique 121-122, 309-323, 1985.
Siegel, C. L. "Über die Klassenzahl quadratischer Zahlkörper." Acta. Arith. 1, 83-86, 1936.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|