


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-6-2019
Date: 18-8-2018
Date: 27-4-2018
|
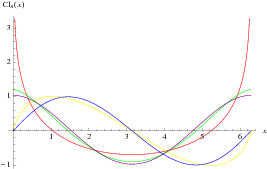
Define
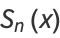 |
 |
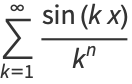 |
(1) |
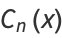 |
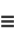 |
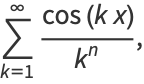 |
(2) |
then the Clausen functions are defined by
 |
(3) |
sometimes also written as 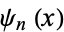 (Arfken 1985, p. 783).
(Arfken 1985, p. 783).
Then the Clausen function 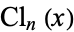 can be given symbolically in terms of the polylogarithm as
can be given symbolically in terms of the polylogarithm as
![Cl_n(x)={1/2i[Li_n(e^(-ix))-Li_n(e^(ix))] n even; 1/2[Li_n(e^(-ix))+Li_n(e^(ix))] n odd.](http://mathworld.wolfram.com/images/equations/ClausenFunction/NumberedEquation2.gif) |
(4) |
For 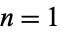 , the function takes on the special form
, the function takes on the special form
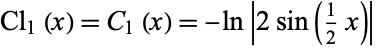 |
(5) |
and for 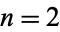 , it becomes Clausen's integral
, it becomes Clausen's integral
![Cl_2(x)=S_2(x)=-int_0^xln[2sin(1/2t)]dt.](http://mathworld.wolfram.com/images/equations/ClausenFunction/NumberedEquation4.gif) |
(6) |
The symbolic sums of opposite parity are summable symbolically, and the first few are given by
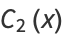 |
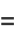 |
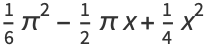 |
(7) |
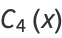 |
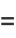 |
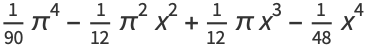 |
(8) |
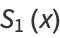 |
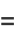 |
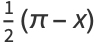 |
(9) |
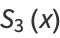 |
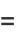 |
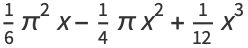 |
(10) |
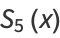 |
 |
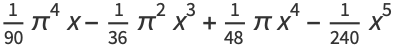 |
(11) |
for  (Abramowitz and Stegun 1972).
(Abramowitz and Stegun 1972).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Clausen's Integral and Related Summations" §27.8 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 1005-1006, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 89-90, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, p. 27, 2004.
Borwein, J. M.; Broadhurst, D. J.; and Kamnitzer, J. "Central Binomial Sums, Multiple Clausen Values and Zeta Functions." Exp. Math. 10, 25-41, 2001.
Clausen, R. "Über die Zerlegung reeller gebrochener Funktionen." J. reine angew. Math. 8, 298-300, 1832.
Grosjean, C. C. "Formulae Concerning the Computation of the Clausen Integral 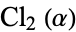 ." J. Comput. Appl. Math. 11, 331-342, 1984.
." J. Comput. Appl. Math. 11, 331-342, 1984.
Jolley, L. B. W. Summation of Series. London: Chapman, 1925.
Lewin, L. Dilogarithms and Associated Functions. London: Macdonald, pp. 170-180, 1958.
Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland, 1981.
Wheelon, A. D. A Short Table of Summable Series. Report No. SM-14642. Santa Monica, CA: Douglas Aircraft Co., 1953.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|