


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-8-2018
Date: 25-7-2019
Date: 18-9-2019
|
In 1757, V. Riccati first recorded the generalizations of the hyperbolic functions defined by
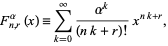 |
(1) |
for 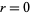 , ...,
, ..., 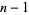 , where
, where 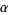 is complex, with the value at
is complex, with the value at 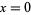 defined by
defined by
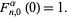 |
(2) |
This is called the 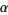 -hyperbolic function of order
-hyperbolic function of order 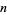 of the
of the 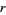 th kind. The functions
th kind. The functions 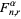 satisfy
satisfy
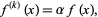 |
(3) |
where
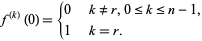 |
(4) |
In addition,
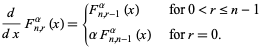 |
(5) |
The functions give a generalized Euler formula
![e^(RadicalBox[alpha, n])=sum_(r=0)^(n-1)(RadicalBox[alpha, n])^rF_(n,r)^alpha(x).](http://mathworld.wolfram.com/images/equations/GeneralizedHyperbolicFunctions/NumberedEquation6.gif) |
(6) |
Since there are 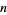
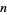 th roots of
th roots of 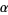 , this gives a system of
, this gives a system of 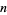 linear equations. Solving for
linear equations. Solving for 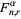 gives
gives
![F_(n,r)^alpha(x)=1/n(RadicalBox[alpha, n])^(-r)sum_(k=0)^(n-1)omega_n^(-rk)exp(omega_n^kRadicalBox[alpha, n]x),](http://mathworld.wolfram.com/images/equations/GeneralizedHyperbolicFunctions/NumberedEquation7.gif) |
(7) |
where
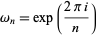 |
(8) |
is a primitive root of unity.
The Laplace transform is
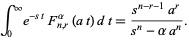 |
(9) |
The generalized hyperbolic function is also related to the Mittag-Leffler function 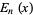 by
by
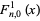 |
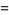 |
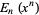 |
(10) |
 |
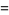 |
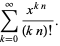 |
(11) |
The values 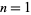 and
and 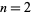 give the exponential and circular/hyperbolic functions (depending on the sign of
give the exponential and circular/hyperbolic functions (depending on the sign of 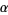 ), respectively.
), respectively.
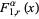 |
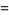 |
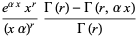 |
(12) |
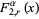 |
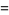 |
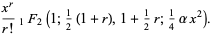 |
(13) |
In particular
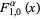 |
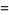 |
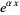 |
(14) |
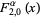 |
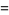 |
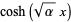 |
(15) |
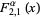 |
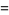 |
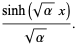 |
(16) |
For 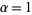 , the first few functions are
, the first few functions are
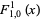 |
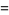 |
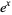 |
(17) |
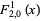 |
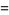 |
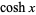 |
(18) |
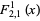 |
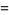 |
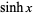 |
(19) |
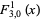 |
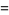 |
![1/3[e^x+2e^(-x/2)cos(1/2sqrt(3)x)]](http://mathworld.wolfram.com/images/equations/GeneralizedHyperbolicFunctions/Inline51.gif) |
(20) |
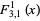 |
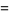 |
![1/3[e^x+2e^(-x/2)cos(1/2sqrt(3)x+1/3pi)]](http://mathworld.wolfram.com/images/equations/GeneralizedHyperbolicFunctions/Inline54.gif) |
(21) |
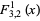 |
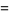 |
![1/3[e^x+2e^(-x/2)cos(1/2sqrt(3)x-1/3pi)]](http://mathworld.wolfram.com/images/equations/GeneralizedHyperbolicFunctions/Inline57.gif) |
(22) |
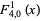 |
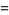 |
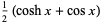 |
(23) |
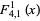 |
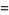 |
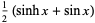 |
(24) |
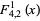 |
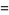 |
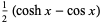 |
(25) |
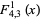 |
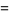 |
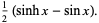 |
(26) |
REFERENCES:
Kaufman, H. "A Biographical Note on the Higher Sine Functions." Scripta Math. 28, 29-36, 1967.
Muldoon, M. E. and Ungar, A. A. "Beyond Sin and Cos." Math. Mag. 69, 3-14, 1996.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Ungar, A. "Generalized Hyperbolic Functions." Amer. Math. Monthly 89, 688-691, 1982.
Ungar, A. "Higher Order Alpha-Hyperbolic Functions." Indian J. Pure. Appl. Math. 15, 301-304, 1984.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|