Inverse Nome

Solving the nome 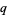 for the parameter  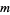gives

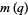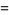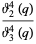			(1)
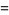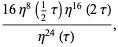			(2)

where 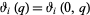 is a Jacobi theta function,  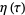is the Dedekind eta function, and  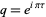is the nome.

The inverse nome function is essentially the same as the elliptic lambda function, the difference being that elliptic lambda function is a function of the half-period ratio , while the inverse nome is a function of the nome 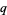, where  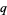is itself a function of .

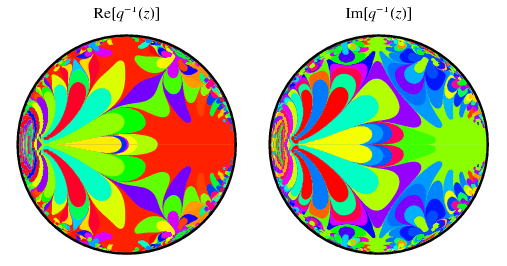
The inverse nome is implemented as InverseEllipticNomeQ[q] in the Wolfram Language.

As a rule, inverse and direct functions satisfy the relation 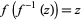-for example, 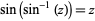. The inverse nome is an exception to this rule due to a historical mistake made more a century ago. In particular, the inverse nome and nome itself are connected by the opposite relation .

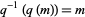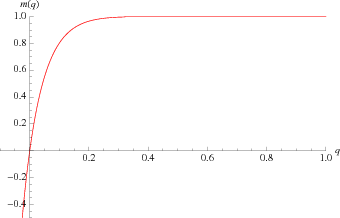
Special values include

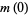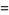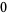			(3)
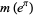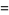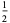			(4)
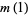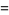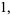			(5)

although strictly speaking, 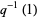 is not defined at 1 because  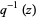is a modular function, therefore has a dense set of singularities on the unit circle, and is therefore only defined strictly inside the unit circle.

It has series

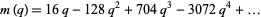(6)

(OEIS A115977).

It satisfies

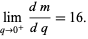(7)

REFERENCES:

Sloane, N. J. A. Sequence A115977 in "The On-Line Encyclopedia of Integer Sequences."

Trott, M. Graphica 1: The World of Mathematica Graphics. The Imaginary Made Real: The Images of Michael Trott. Champaign, IL: Wolfram Media, pp. 66 and 89, 1999.