المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Ker |
 2004
 02:00 مساءً
date: 25-3-2019 |
Author : Abramowitz, M. and Stegun, I. A. 
Book or Source : "Kelvin Functions." §9.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover 
Page and Part : ...|
Read More
Date: 21-7-2019
1454
Date: 24-6-2019
1821
Date: 23-8-2018
5864
|
The symbol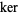 
has at least two different meanings in mathematics. It can refer to a special function related to Bessel functions, or (written either with a capital or lower-case "K"), it can denote a kernel.
The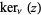 
function is defined as the real part of
 |
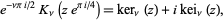(1) |
where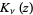 
is a modified Bessel function of the second kind. Therefore
![ker_nu(z)=R[e^(-nupii/2)K_nu(ze^(pii/4))],](http://mathworld.wolfram.com/images/equations/Ker/NumberedEquation2.gif) |
(2) |
where ![R[z]](http://mathworld.wolfram.com/images/equations/Ker/Inline4.gif)
is the real part.
It is implemented in the Wolfram Language as KelvinKer[nu, z].
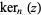has a complicated series given by Abramowitz and Stegun (1972, p. 379).
850
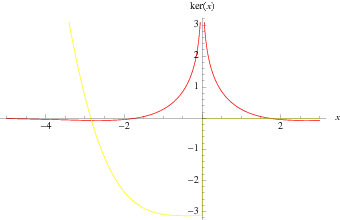
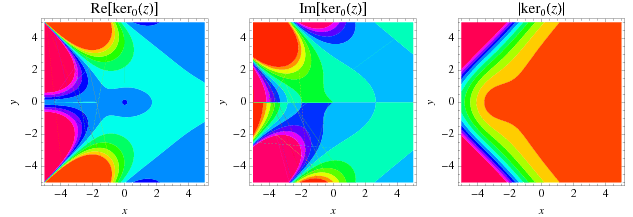
The special case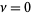 
is commonly denoted 
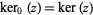and has the plot shown above. 
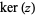has the series expansion
![ker(x)=-ln(1/2x)ber(x)+1/4pibei(x)
+sum_(k=0)^infty(-1)^k(psi(2k+1))/([(2k)!]^2)(1/4x^2)^(2k),](http://mathworld.wolfram.com/images/equations/Ker/NumberedEquation3.gif) |
(3) |
where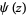 
is the digamma function (Abramowitz and Stegun 1972, p. 380).
"ker" is also an abbreviation for "group kernel" of a group homomorphism.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Kelvin Functions." §9.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 379-381, 1972.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Kelvin Functions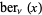 
, 
, 
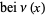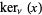and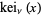 
." §1.7 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 29-30, 1990.a
|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|
