


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-2-2019
Date: 2-2-2016
Date: 23-1-2019
|
Given a polynomial
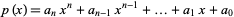 |
(1) |
of degree  with roots
with roots  ,
,  , ...,
, ..., 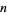 and a polynomial
and a polynomial
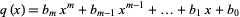 |
(2) |
of degree 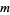 with roots
with roots 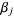 ,
, 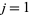 , ...,
, ..., 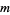 , the resultant
, the resultant 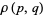 , also denoted
, also denoted 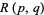 and also called the eliminant, is defined by
and also called the eliminant, is defined by
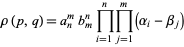 |
(3) |
(Trott 2006, p. 26).
Amazingly, the resultant is also given by the determinant of the corresponding Sylvester matrix.
Kronecker gave a series of lectures on resultants during the summer of 1885 (O'Connor and Robertson 2005).
An important application of the resultant is the elimination of one variable from a system of two polynomial equations (Trott 2006, p. 26).
The resultant of two polynomials can be computed using the Wolfram Language function Resultant[poly1, poly2, var]. This command accepts the following methods: Automatic, SylvesterMatrix, BezoutMatrix, Subresultants, and Modular, where the optimal choice depends dramatically on the concrete polynomial pair under consideration and typically requires some experimentation. For high-order univariate polynomials over the integers, the option setting Modular is frequently the fastest (Trott 2006, p. 29).
There exists an algorithm similar to the Euclidean algorithm for computing resultants (Pohst and Zassenhaus 1989).
Resultants for a few simple pairs of polynomials include
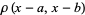 |
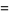 |
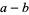 |
(4) |
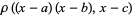 |
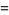 |
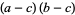 |
(5) |
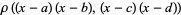 |
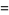 |
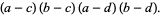 |
(6) |
Given 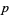 and
and 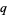 , then
, then
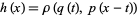 |
(7) |
is a polynomial of degree 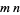 , having as its roots all sums of the form
, having as its roots all sums of the form 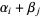 .
.
REFERENCES:
Apostol, T. M. "Resultants of Cyclotomic Polynomials." Proc. Amer. Math. Soc. 24, 457-462, 1970.
Apostol, T. M. "The Resultant of the Cyclotomic Polynomials 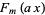 and
and 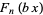 ." Math. Comput. 29, 1-6, 1975.
." Math. Comput. 29, 1-6, 1975.
Bikker, P. and Uteshev, A. Y. "On the Bézout Construction of the Resultant." J. Symb. Comput. 28, 45-88, 1999.
Bykov, V.; Kytmanov, A.; Lazman, M.; and Passare, M. (Eds.). Elimination Methods in Polynomial Computer Algebra. Dordrecht, Netherlands: Kluwer, 1998.
Childs, L. A Concrete Introduction to Higher Algebra. New York: Springer-Verlag, 1992.
Cohen, H. "Resultants and Discriminants." §3.3.2 in A Course in Computational Algebraic Number Theory. New York: Springer-Verlag, pp. 119-123, 1993.
Cohen, J. S. Computer Algebra and Symbolic Computation: Mathematical Methods. Wellesley: A K Peters, 2003.
Davenport, J. H.; Siret, Y.; and Tournier, E. Computer Algebra: Systems and Algorithms for Algebraic Computations. London: Academic Press, 1993.
Gelfand, I. M.; Kapranov, M.; and Zelevinsky, A. Discriminants, Resultants and Multidimensional Resultants. Boston: Birkhäuser, 1994.
Maculay, F. S. The Algebraic Theory of Modular Systems. Cambridge: Cambridge University Press, 1916.
O'Connor, J. J. and Robertson, E. F. "Henry Burchard Fine." August 2005. http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Fine_Henry.html.
Pohst, M. and Zassenhaus, H. Algorithmic Algebraic Number Theory. Cambridge, England: Cambridge University Press, 1989.
Prasalov, V. V. Polynomials. Berlin: Springer, 2004.
Simpson, J. A. and Weiner, E. S. C. (Preparers). The Compact Oxford English Dictionary, 2nd ed. Oxford, England: Clarendon Press, p. 503, 1992.
Sturmfels, B. In Applications of Computational Algebraic Geometry. American Mathematical Society Short Course January 6-7, 1997 San Diego, California (Ed. D. A. Cox and B. Sturmfels). Providence, RI: Amer. Math. Soc., 1997.
Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, pp. 26-29, 2006. http://www.mathematicaguidebooks.org/.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, p. 348, 1991.
Wee, C. E. and Goldman, R. N. IEEE Comput. Graphics Appl. No. 1, 69, 1995.
Wee, C. E. and Goldman, R. N. IEEE Comput. Graphics Appl. No. 3, 60, 1995.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|