Area Principle

There are at least two results known as "the area principle."

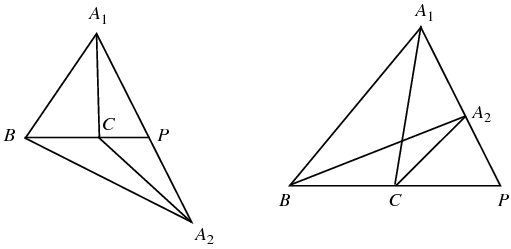
The geometric area principle states that

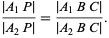(1)

This can also be written in the form

(2)

where

(3)

is the ratio of the lengths  and  for 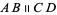 with a plus or minus sign depending on if these segments have the same or opposite directions, and

(4)

is the ratio of signed areas of the triangles. Grünbaum and Shepard (1995) show that Ceva's theorem, Hoehn's theorem, and Menelaus' theorem are the consequences of this result.

The area principle of complex analysis states that if 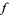 is a schlicht function and if

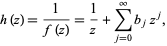(5)

then

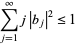(6)

(Krantz 1999, p. 150).

REFERENCES:

Grünbaum, B. and Shepard, G. C. "Ceva, Menelaus, and the Area Principle." Math. Mag. 68, 254-268, 1995.

Krantz, S. G. "Schlicht Functions." §12.1.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 149, 1999.