


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-5-2018
Date: 22-9-2019
Date: 26-7-2019
|
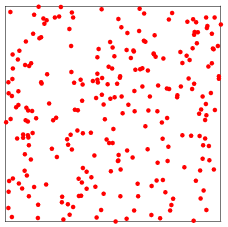
Picking two independent sets of points  and
and 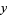 from a unit uniform distribution and placing them at coordinates
from a unit uniform distribution and placing them at coordinates 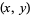 gives points uniformly distributed over the unit square.
gives points uniformly distributed over the unit square.
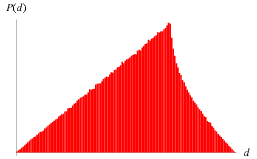
The distribution of distances 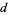 from a randomly selected point in the unit square to its center is illustrated above.
from a randomly selected point in the unit square to its center is illustrated above.
The expected distance to the square's center is
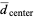 |
 |
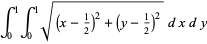 |
(1) |
 |
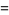 |
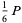 |
(2) |
 |
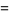 |
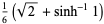 |
(3) |
 |
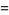 |
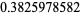 |
(4) |
(Finch 2003, p. 479; OEIS A103712), where 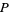 is the universal parabolic constant. The expected distance to a fixed vertex is given by
is the universal parabolic constant. The expected distance to a fixed vertex is given by
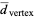 |
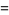 |
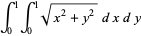 |
(5) |
 |
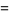 |
![1/3[sqrt(2)+sinh^(-1)1],](http://mathworld.wolfram.com/images/equations/SquarePointPicking/Inline23.gif) |
(6) |
which is exactly twice 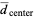 .
.
The expected distances from the closest and farthest vertices are given by
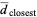 |
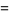 |
![1/(24)[2+sqrt(2)sinh^(-1)1]](http://mathworld.wolfram.com/images/equations/SquarePointPicking/Inline27.gif) |
(7) |
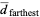 |
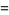 |
![1/(24)[18-4sqrt(10)-8sqrt(2)csch^(-1)2+9sqrt(2)sinh^(-1)1-sqrt(2)sinh^(-1)2].](http://mathworld.wolfram.com/images/equations/SquarePointPicking/Inline30.gif) |
(8) |
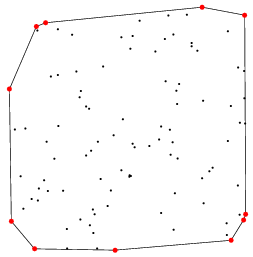
Pick 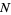 points at randomly in a unit square and take the convex hull
points at randomly in a unit square and take the convex hull 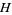 . Let
. Let 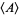 be the expected area of
be the expected area of 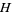 ,
, 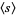 the expected perimeter, and
the expected perimeter, and 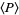 the expected number of vertices of
the expected number of vertices of 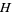 . Then
. Then
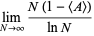 |
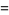 |
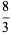 |
(9) |
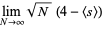 |
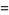 |
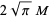 |
(10) |
 |
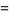 |
![(4sqrt(2)pi^2)/([Gamma(1/4)]^2)](http://mathworld.wolfram.com/images/equations/SquarePointPicking/Inline46.gif) |
(11) |
 |
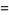 |
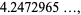 |
(12) |
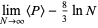 |
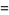 |
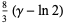 |
(13) |
 |
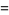 |
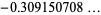 |
(14) |
(OEIS A096428 and A096429), where 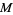 is the multiplicative inverse of Gauss's constant,
is the multiplicative inverse of Gauss's constant, 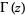 is the gamma function, and
is the gamma function, and 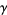 is the Euler-Mascheroni constant (Rényi and Sulanke 1963, 1964; Finch 2003, pp. 480-481).
is the Euler-Mascheroni constant (Rényi and Sulanke 1963, 1964; Finch 2003, pp. 480-481).
In addition,
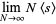 |
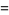 |
![[8/5(3+4sqrt(2))-(32)/5ln(1+sqrt(2))-(8pi^4)/([Gamma(1/4)]^4)]+I_1+I_2+I_3](http://mathworld.wolfram.com/images/equations/SquarePointPicking/Inline61.gif) |
(15) |
 |
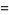 |
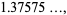 |
(16) |
where
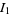 |
 |
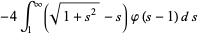 |
(17) |
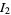 |
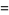 |
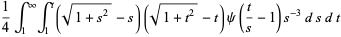 |
(18) |
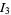 |
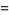 |
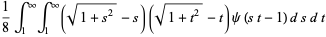 |
(19) |
and
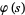 |
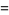 |
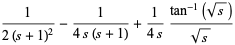 |
(20) |
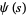 |
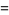 |
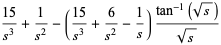 |
(21) |
(Groeneboom 1988; Cabo and Groeneboom 1994; Keane 2000; Finch 2003, p. 481).
REFERENCES:
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E. "Box Integrals." Preprint. Apr. 3, 2006.
Cabo, A. J. and Groeneboom, P. "Limit Theorems for Functionals of Convex Hulls." Probab. Th. Related Fields 100, 31-55, 1994.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 480-481, 2003.
Groeneboom, P. "Limit Theorems for Complex Hulls." Probab. Th. Related Fields 79, 327-368, 1988.
Heuter, I. "Limit Theorems for the Convex Hull of Random Points in Higher Dimensions." Trans. Amer. Math. Soc. 351, 4337-4363, 1999.
Keane, J. "Convex Hull Integrals and the 'Ubiquitous Constant.' " Unpublished note, 2000.
Rényi, A. and Sulanke, R. "Über die konvexe Hülle von 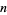 zufällig gewählten Punkten, I." Z. Wahrscheinlichkeits 2, 75-84, 1963.
zufällig gewählten Punkten, I." Z. Wahrscheinlichkeits 2, 75-84, 1963.
Rényi, A. and Sulanke, R. "Über die konvexe Hülle von 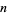 zufällig gewählten Punkten, II." Z. Wahrscheinlichkeits 3, 138-147, 1964.
zufällig gewählten Punkten, II." Z. Wahrscheinlichkeits 3, 138-147, 1964.
Sloane, N. J. A. Sequences A096428, A096429, and A103712 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|