الطاقة الميكانيكية لمنظومة الجسم والنابض (Mechanical Energy for Block – Spring System)

أن كلمة منظومة (System) تعني ارتباط جسمين او اكثر بحيث يكونون وحدة واحدة. وهنا سوف نوضح أربعة أوضاع لحساب الطاقة الميكانيكية لمنظومة الجسم والنابض كما في الشكل (1-1).

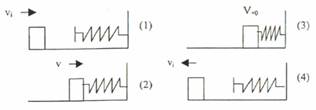
الشكل (1-1)

الحالة (1): تمثل جسم يتحرك بسرعة (v_i) باتجاه نابض في حالة استقرار دون أن يلامسه. الطاقة الميكانيكية للمنظومة تساوي مجموع الطاقة الميكانيكية للجسم والنابض:

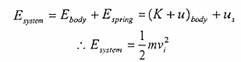
علماً ان u_body = 0 لأن الجسم يتحرك على المحور السيني (لا يوجد تغير في الإحداثيات الصادية).

كما أن : u_s = 0 حيث النابض لم يتعرض لضغط او سحب (النابض يتملك طاقة وضع فقط ولا يتملك طاقة حركية أبداً، أي أن K_s = 0).

الحالة (2): الجسم يصطدم ويستمر بالضغط عليه مما يولد طاقة وضع داخل النابض ، u_s = ½ kx² ، حيث x تمثل مقدار إزاحة النابض عن نقطة الاستقرار. وبذلك تكون الطاقة الميكانيكية للمنظومة تساوي:

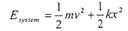
حيث u_body = 0.

الحالة (3): الجسم يولد اكبر ضغط على النابض ثم يتوقف عن الحركة (v = 0)، وبذلك تكون الطاقة الميكانيكية للمنظومة تساوي :

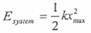
حيث : K_body = 0              ،        u_body = 0

الحالة (4): النابض يدفع الجسم بعيداً عنه بسرعة أولية (v_i) بسبب قوة إرجاع النابض وبعدها يعود النابض إلى وضع الاستقرار، وبذلك تكون الطاقة الميكانيكية مساوية إلى:                

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل