
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
العزم الدوراني (The Torque)
المؤلف:
د. معن صفاء ابراهيم
المصدر:
الفيزياء الجامعية 101
الجزء والصفحة:
ص 198
15-2-2016
14505
العزم الدوراني (The Torque)
عندما تؤثر قوة (F) على جسم صلب له محور ثابت فسوف يدور الجسم حول هذا المحور. ويمثل ميل القوة لتدوير الجسم بالعزم الدوراني، انظر الشكل (1-1)، حيث يتضح أن القوة المؤثرة على الجسم F يمكن تحليلها إلى مركبتين ، واحدة عمودية على المستقيم r، والثانية موازية له، وكما يلي:

ويعرف العزم الدوراني على أنه حاصل ضرب مركبة القوة العمودية على محور الدوران في المسافة بين المركبة العمودية إلى نقطة التثبيت وكما يلي:
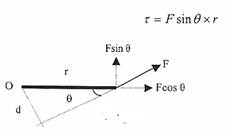
الشكل ((1-1
ويمكن أن نستنتج ببساطة من الشكل أن (sin θ = d/r)،إذاً:

حيث d تمثل المسافة العمودية بين نقطة التثبيت (O) والخط الوهمي لتأثير القوة F التي تحاول تدوير الجسم. ولقد تم الاتفاق على أن يكون العزم الدوراني موجباً (+)τ إذا دار الجسم عكس حركة عقرب الساعة، ويكون سالباً (-)τ إذا دار الجسم مع حركة عقرب الساعة.

الشكل (1-2)
الشكل (1-2) يمثل قوتان تحاولان تدوير جسم صلب حول نقطة (O)، حيث القوة F1 تحاول تدويره عكس حركة عقارب الساعة، والقوة F2 تحاول تدويره باتجاه حركة عقارب الساعة. وحيث أن كلاً من القوتين تمتلك عزماً دورانياً هو:
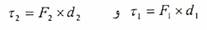
وبذلك تكون محصلة العزم الدوراني تساوي المجموع الجبري لعزوم القوى المؤثرة على الجسم كما يلي:

وحيث أن القوة والإزاحة هي كميات متجهة، لذا فإن العزم كمتجه يمثل حاصل ضرب تقاطعي لمتجهتين (The Cross Product of Two Vectors) هما: متجه القوة ومتجه الإزاحة، حيث يمكن الاستفادة من خاصية ضرب المتجهات التقاطعي لإيجاد العزم المتجه في حالة أن القوة والإزاحة تعرف بدلالة المتجهات الأحادية (The Unit Vectors). ومن المعلوم أن حاصل ضرب متجهين تقاطعياً يساوي متجه ثالث له قيمة وله اتجاه، حيث أن ناتج ضرب المتجه A بالمتجه B تقاطعياً هو متجه ثالث يمثله المتجه C وكما يلي:
B = C× A
حيث المتجه C له قيمة تساوي:
C = A×B=AB sinθ
فإذا عرف المتجهين بدلالة المتجهات الأحادية، يمكن إيجاد قيمة المتجه A والمتجه B، ومن معرفة الزاوية θ المحصورة بين المتجهين، يمكن إيجاد قيمة المتجه C لقيمة واتجاه فيمكن إيجاده طريقة ضرب المصفوفات (Matrixes) خاصة عندما لا تكون الزاوية بينهما المتجهين معلومة وذلك كما يلي:
إذا افترضنا أن المتجه الأول يساوي A = Axi + Ayj + Azk والمتجه الثاني يساوي B = Bxi + Byj + Bzk ، فإن حاصل ضرب المتجهين تقاطعياً بطريقة المصفوفات يساوي المتجه C الذي يمكن إيجاده كما يلي:
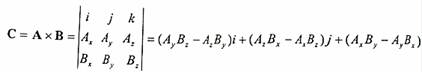
وإذا كان المتجه C يمثل متجه العزم الدوراني للجسم الذي مر قيمة واتجاه، وذلك طبعاً بعد الاستفادة من خواص الضرب التقاطعي للمتجهات الأحادية حيث:
1) يكون حاصل ضرب المتجهات الأحادية كما يلي:
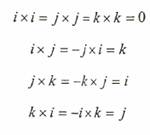
2) A×B = -B×A
3) إذا كان A يوازي B ( أي أن θ = 180o or θ= 0o) ، فإن B = 0×A حيث Sin θ = 0o.
4) إذا كان A عمودياً على B، فإن (θ = 90o)، فإن B = AB×A حيث sin 90o = 1.
5) يمكن القول أن: C×A+B×A = (B+C)×A
6) مشتقة ضرب متجهين تساوي:
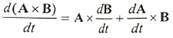
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















