يتكون العديد من النبائط البسيطة والمهمة (مثلا، نظام لكتلة وأوتار وبكرة) من عدة أجزاء متصلة بأوتار أو حبال قبل تحليل مثل هذه النبائط، علينا فهم المقصود بالوتر وماذا يعني الشد فيه. لأغراض مفاهيمية دعنا نقسم الوتر إلى جزءين: A وB، بواسطة مستوى تخيلي عمودي على الوتر عند نقطة اختيارية (ما نؤكد على أن المستوى ما هو إلا بناء رياضياتي لا يتلف الوتر!) يؤثر الجزء B بقوة  على A (شكل 2–9)، ومن القانون الثالث يؤثر A بقوة – على B.

يجب أن يكون  موازيًا (مماسيًّا) للوتر ويجب أن يشير في الاتجاه من A إلى B. تميز هاتان الخاصيتان الوتر عن القضيب. يمكن لجزء من القضيب أن يؤثر بقوة عرضية (تسمى قوة قص) على الجزء المجاور، بالإضافة إلى قوة موازية للقضيب. في حالة القضيب، يمكن للقوة الموازية المؤثرة بواسطة B على A أن تُشير في الاتجاه من A إلى B (ونقول في هذه الحالة إن B تسحب A) أو من B إلى A (ونقول في هذه الحالة إن B تدفع A). لا يمكن لجزء من وتر ما أن يؤثر بقوة عرضية على الجزء المجاور ويمكنه فقط سحب (وليس دفع) الجزء المجاور.

شكل 2–9: مفاهيميًّا، نقسم الوتر إلى قطعتين بواسطة مستوى تخيلي. يؤثر B بقوة  على A ويؤثر A بقوة – على B. المقدار المشترك لهاتين القوتين يُسَمَّى الشد في هذه النقطة من الوتر.

يسمى مقدار (المساوي، بالطبع، لمقدار –) بالشد في الوتر عند النقطة محل الدراسة. سوف نرى أنه في ظل ظروف معينة يكون الشد كما هو عند جميع النقاط في وتر ما. رغم ذلك، ليس هذا هو الحال دائمًا (انظر مثال 2–6). أحد الأسئلة التي تطرح كثيرًا، لكن ليس له بالفعل معنى دقيق، هو «في أي اتجاه يؤثر الشد؟» فالشد هو المقدار المشترك لقوتين؛ تؤثر إحداهما على A وتتجه من A إلى B، وتؤثر القوة الأخرى على B وتتجه من B إلى A.

مثال 2–6 (شد في وتر بواسطة ثقل). هَب أن لدينا كتلة وزنها W معلقة من السقف بواسطة وتر رأسي وزنه لكل وحدة طول هو w (انظر شكل 2–10). نرغب في إيجاد الشد عند نقطة P على مسافة × من الطرف السفلي للوتر. نُعرِّف «النظام» محل الدراسة بأنه الكتلة بالإضافة إلى جزء الوتر أسفل P. هناك قوتان خارجيتان تؤثران على النظام: تؤثر الكرة الأرضية بقوة جاذبية لأسفل مقدارها W + wx ويؤثر جزء الوتر فوق P بقوة لأعلى مقدارها هو الشد T عند نقطة P. وبما أنه يجب أن تكون القوة الكلية الخارجية صفرًا، نجد أن T=W + wx. وبذلك لا يكون الشد هو ذاته عند جميع نقاط الوتر وتكون قيمته العظمى عند أعلى نقطة في الوتر. إذا كان الوتر جميع بلا وزن 0 = w فإن الشد يكون كما هو عند جميع نقط الوتر.

وبوجه أعم ، حتى لو كان الوتر يمر على بكرات، يمكننا أن نبين أن الشد يكون كما هو عند جميع نقاط الوتر بشرط أن يكون الوتر بلا وزن، وبشرط أن يكون سطح التماس بين الوتر والبكرة أملس. تكون هذه الجملة صحيحة حتى في حالات عدم الاتزان، ولكننا الآن سنبرهن عليها فقط عندما يكون الوتر في حالة اتزان اعتبر قطعة قصيرة جدًّا من الوتر. يؤثر باقي الوتر بقوى على طرفيه. بالإضافة إلى ذلك، إذا كانت القطعة متماسة مع سطح أملس، فإن السطح قد يؤثر بقوة عمودية على القطعة. وإذا كان الوتر بلا وزن، فلن تكون هناك قوة جاذبية مؤثرة على القطعة. وإذا كانت القطعة في حالة اتزان يجب أن تتلاشى القوة الكلية المؤثرة عليها. وبصورة خاصة، أن يجب تتلاشى محصلة جميع القوى المؤثرة على طول الاتجاه الموازي للقطعة. وهذا يقتضي ضمنًا أن تكون قوتا الشد عند الطرفين متساويتين. ينتج من ذلك أن الشد متماثل عند جميع نقط الوتر.

سوف يُفترض من الآن فصاعدًا إلا إذا ذُكر غير ذلك، في المثال القادم وجميع الأمثلة التالية التي تتعلق بالحبال والبكرات أو إحداهما، أن وزن الحبال يمكن إهماله وأن البكرات ملساء؛ وبناءً على ذلك يكون الشد متماثلا عند جميع نقط الحبل. وسوف يُفتَرَض أيضًا أن البكرات بدون وزن ما لم يُنص على غير ذلك.

مثال 2–7 (تحليل) نظام بكرات بسيط. يبين شكل 2–11 (أ) نظام بكرات بسيطًا. لاحظ أن البكرة B مُثبتة في الفضاء، بينما تتحرك البكرة A لأعلى ولأسفل مع الوزن W. السؤال البدهي هو: ما القوة التي يجب أن تؤثر على نهاية الحبل لكي تحافظ على الاتزان؟

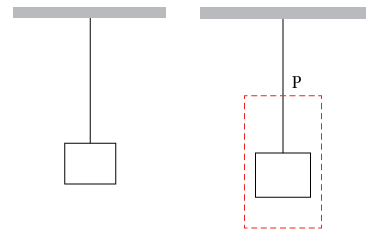
شکل 2–10: كتلة وزنها W معلقة بواسطة وتر وزنه w لكل وحدة طول. لإيجاد الشد عند نقطة P سيكون من المفيد تعريف النظام المعني بأنه كل شيء أسفل P.

أولًا، علينا أن نعترف بأن الشد في الحبل يساوي F. لإثبات ذلك، نتخذ قطعة الحبل المحتواة داخل الصندوق المتقطع في شكل 2–11 (ب) لتكون نظامنا المعني بالدراسة. القوتان الخارجيتان الوحيدتان اللتان تؤثران على هذا النظام هما القوة F لأسفل وقوة لأعلى مقدارها T تؤثر بواسطة باقي الحبل على نهاية الطرف العلوي للقطعة. وبما أنه يجب للقوة الكلية المؤثرة على القطعة أن تتلاشى، نجد أن T = F.

لحساب F نُعَرِّف نظامنا بأنه محتويات الصندوق المتقطع في شكل 2–11(ج). القوى الخارجية الوحيدة المؤثرة على هذا النظام (انظر شكل 2–11(د)) هي قوة سحب الجاذبية لأسفل على الكتلة (يُفترض هنا أن البكرتين بدون وزن) والقوى المؤثرة على قطعة الحبل التي على شكل حرف U لأعلى بواسطة باقي الحبل. شرط الاتزان هو 0 = 2T – W. وبما أن T = F، نجد أن 2/F = W. وبذلك يمكن لقوة مؤثرة على نهاية طرف الحبل مقدارها 50 رطلًا أن تُبقي على كتلة وزنها 100 رطل في حالة اتزان. يمكن تلخيص هذه الحقيقة في القول بأن نظام البكرات يضاعف الفائدة الميكانيكية. لاحظ أنه إذا استُخدم نظام البكرات لرفع الوزن W، فإنه يجب أن تُشَد نهاية طرف الحبل الحر لأسفل لمسافة تساوي ضعف المسافة التي ارتفعها W. يسمح لك نظام البكرات بإنجاز المهمة باستخدام قوة أقل، لكن عليك أن تؤثر بهذه القوة لمسافة أطول. يوضح لنا هذا مبدأ أعم بكثير جدًّا يسمى «حفظ الطاقة»، وهو التعبير الفيزيائي لمقولة: «لا يمكنك الحصول على شيء بدون مقابل.»

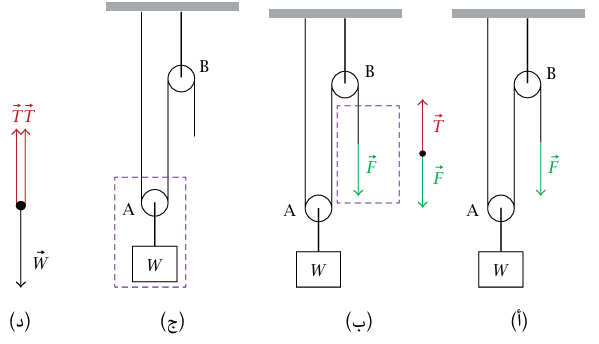
شكل 2–11: (أ) نظام بكرات بسيط في المثال 2–7 (ب) يبين اعتبار مخطط الجسم الحر للنظام المحاط بالصندوق المتقطع أن الشد في الحبل يكون مساويًا للقوة  المؤثرة عند الطرف. (ج) من المفيد لحساب F أن نُعَرِّف نظامنا بأنه محتويات الصندوق المتقطع. (د) مخطط الجسم الحر للنظام المعرف في شكل 2–11(ج).

يمكننا تصميم أنظمة بكرات ذات فائدة ميكانيكية اختيارية كبيرة باستخدام ترتيبات مناسبة من الحبال والبكرات (انظر شكل 2–12).

شكل 2–12: كل من هذين الترتيبين للبكرات يوفر أربعة أضعاف الفائدة الميكانيكية.