Now we are able to describe what it is that determines the “quality” of a musical tone. It is the relative amounts of the various harmonics—the values of the a’s and b’s. A tone with only the first harmonic is a “pure” tone. A tone with many strong harmonics is a “rich” tone. A violin produces a different proportion of harmonics than does an oboe.

We can “manufacture” various musical tones if we connect several “oscillators” to a loudspeaker. (An oscillator usually produces a nearly pure simple harmonic function.) We should choose the frequencies of the oscillators to be ω, 2ω, 3ω, etc. Then by adjusting the volume control on each oscillator, we can add in any amount we wish of each harmonic—thereby producing tones of different quality. An electric organ works in much this way. The “keys” select the frequency of the fundamental oscillator and the “stops” are switches that control the relative proportions of the harmonics. By throwing these switches, the organ can be made to sound like a flute, or an oboe, or a violin.

It is interesting that to produce such “artificial” tones we need only one oscillator for each frequency—we do not need separate oscillators for the sine and cosine components. The ear is not very sensitive to the relative phases of the harmonics. It pays attention mainly to the total of the sine and cosine parts of each frequency. Our analysis is more accurate than is necessary to explain the subjective aspect of music. The response of a microphone or other physical instrument does depend on the phases, however, and our complete analysis may be needed to treat such cases.

The “quality” of a spoken sound also determines the vowel sounds that we recognize in speech. The shape of the mouth determines the frequencies of the natural modes of vibration of the air in the mouth. Some of these modes are set into vibration by the sound waves from the vocal chords. In this way, the amplitudes of some of the harmonics of the sound are increased with respect to others. When we change the shape of our mouth, harmonics of different frequencies are given preference. These effects account for the difference between an “e–e–e” sound and an “a–a–a” sound.

We all know that a particular vowel sound—say “e–e–e”—still “sounds like” the same vowel whether we say (or sing) it at a high or a low pitch. From the mechanism we describe, we would expect that particular frequencies are emphasized when we shape our mouth for an “e–e–e,” and that they do not change as we change the pitch of our voice. So the relation of the important harmonics to the fundamental—that is, the “quality”—changes as we change pitch. Apparently, the mechanism by which we recognize speech is not based on specific harmonic relationships.

What should we say now about Pythagoras’ discovery? We understand that two similar strings with lengths in the ratio of 2 to 3 will have fundamental frequencies in the ratio 3 to 2. But why should they “sound pleasant” together? Perhaps we should take our clue from the frequencies of the harmonics. The second harmonic of the lower shorter string will have the same frequency as the third harmonic of the longer string. (It is easy to show—or to believe—that a plucked string produces strongly the several lowest harmonics.)

Perhaps we should make the following rules. Notes sound consonant when they have harmonics with the same frequency. Notes sound dissonant if their upper harmonics have frequencies near to each other but far enough apart that there are rapid beats between the two. Why beats do not sound pleasant, and why unison of the upper harmonics does sound pleasant, is something that we do not know how to define or describe. We cannot say from this knowledge of what sounds good, what ought, for example, to smell good. In other words, our understanding of it is not anything more general than the statement that when they are in unison, they sound good. It does not permit us to deduce anything more than the properties of concordance in music.

It is easy to check on the harmonic relationships we have described by some simple experiments with a piano. Let us label the 3 successive C’s near the middle of the keyboard by C, C′, and C′′, and the G’s just above by G, G′, and G′′. Then the fundamentals will have relative frequencies as follows:

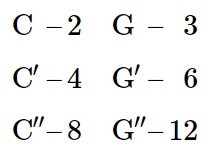
These harmonic relationships can be demonstrated in the following way: Suppose we press C′ slowly—so that it does not sound but we cause the damper to be lifted. If we then sound C, it will produce its own fundamental and some second harmonic. The second harmonic will set the strings of C′ into vibration. If we now release C (keeping C′ pressed) the damper will stop the vibration of the C strings, and we can hear (softly) the note C′ as it dies away. In a similar way, the third harmonic of C can cause a vibration of G′. Or the sixth of C (now getting much weaker) can set up a vibration in the fundamental of G′′.

A somewhat different result is obtained if we press G quietly and then sound C′. The third harmonic of C′ will correspond to the fourth harmonic of G, so only the fourth harmonic of G will be excited. We can hear (if we listen closely) the sound of G′′, which is two octaves above the G we have pressed! It is easy to think up many more combinations for this game.

We may remark in passing that the major scale can be defined just by the condition that the three major chords (F–A–C); (C–E–G); and (G–B–D) each represent tone sequences with the frequency ratio (4:5:6). These ratios—plus the fact that an octave (C–C′, B–B′, etc.) has the ratio 1:2—determine the whole scale for the “ideal” case, or for what is called “just intonation.” Keyboard instruments like the piano are not usually tuned in this manner, but a little “fudging” is done so that the frequencies are approximately correct for all possible starting tones. For this tuning, which is called “tempered,” the octave (still 1:2) is divided into 12 equal intervals for which the frequency ratio is (2)1/12. A fifth no longer has the frequency ratio 3/2, but 27/12=1.499, which is apparently close enough for most ears.

We have stated a rule for consonance in terms of the coincidence of harmonics. Is this coincidence perhaps the reason that two notes are consonant? One worker has claimed that two pure tones—tones carefully manufactured to be free of harmonics—do not give the sensations of consonance or dissonance as the relative frequencies are placed at or near the expected ratios. (Such experiments are difficult because it is difficult to manufacture pure tones, for reasons that we shall see later.) We cannot still be certain whether the ear is matching harmonics or doing arithmetic when we decide that we like a sound.