Interpolation

The computation of points or values between ones that are known or tabulated using the surrounding points or values.

In particular, given a univariate function 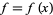, interpolation is the process of using known values  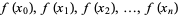to find values for  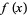at points 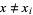, 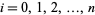. In general, this technique involves the construction of a function  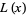called the interpolant which agrees with  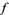at the points  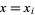and which is then used to compute the desired values.

Unsurprisingly, one can talk about interpolation methods for multivariate functions as well, though these tend to be substantially more involved than their univariate counterparts.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Interpolation." §25.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 878-882, 1972.

Iyanaga, S. and Kawada, Y. (Eds.). "Interpolation." Appendix A, Table 21 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1482-1483, 1980.

Meijering, E. "A Chronology of Interpolation: From Ancient Astronomy to Modern Signal and Image Processing." Proc. IEEE 90, 319-342, 2002. http://bigwww.epfl.ch/publications/meijering0201.pdf.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Interpolation and Extrapolation." Ch. 3 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 99-122, 1992.

Whittaker, E. T. and Robinson, G. "Interpolation with Equal Intervals of the Argument." Ch. 1 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 1-34, 1967.