المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Lyapunov Characteristic Number |
 983
 05:55 مساءً
date: 11-10-2021 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 21-9-2021
1076
Date: 11-2-2016
1066
Date: 19-11-2021
1097
|
Given a Lyapunov characteristic exponent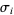 
, the corresponding Lyapunov characteristic number 
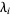is defined as
 |
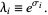(1) |
For an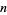 
-dimensional linear map,
 |
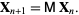(2) |
The Lyapunov characteristic numbers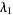 
, ..., 
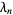are the eigenvalues of the map matrix. For an arbitrary map
 |
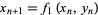(3) |
 |
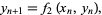(4) |
the Lyapunov numbers are the eigenvalues of the limit
![lim_(n->infty)[J(x_n,y_n)J(x_(n-1),y_(n-1))...J(x_1,y_1)]^(1/n),](https://mathworld.wolfram.com/images/equations/LyapunovCharacteristicNumber/NumberedEquation5.gif) |
(5) |
where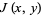 
is the Jacobian
 |
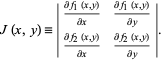(6) |
If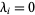 
for all 
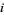, the system is not chaotic. If 
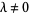and the map is area-preserving (Hamiltonian), the product of eigenvalues is 1.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
