


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-10-2021
Date: 23-9-2021
Date: 16-10-2021
|

The curlicue fractal is a figure obtained by the following procedure. Let 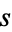 be an irrational number. Begin with a line segment of unit length, which makes an angle
be an irrational number. Begin with a line segment of unit length, which makes an angle 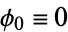 to the horizontal. Then define
to the horizontal. Then define 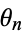 iteratively by
iteratively by
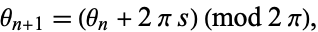 |
with 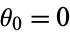 . To the end of the previous line segment, draw a line segment of unit length which makes an angle
. To the end of the previous line segment, draw a line segment of unit length which makes an angle
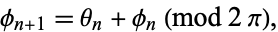 |
to the horizontal (Pickover 1995ab). The result is a fractal, and the above figures correspond to the curlicue fractals with 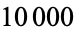 points for the golden ratio
points for the golden ratio 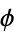 ,
, 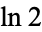 ,
, 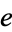 ,
, 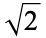 , the Euler-Mascheroni constant
, the Euler-Mascheroni constant 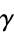 ,
, 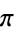 , and the Feigenbaum constant
, and the Feigenbaum constant 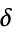 .
.
The temperature of these curves is given in the following table.
| constant | temperature |
golden ratio 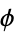 |
46 |
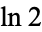 |
51 |
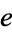 |
58 |
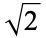 |
58 |
Euler-Mascheroni constant 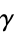 |
63 |
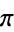 |
90 |
Feigenbaum constant 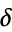 |
92 |
REFERENCES:
Berry, M. and Goldberg, J. "Renormalization of Curlicues." Nonlinearity 1, 1-26, 1988.
Mendès-France, M. "Entropie, dimension et thermodynamique des courbes planes." In Seminar on number theory, Paris 1981-82 (Paris, 1981/1982) (Ed. M.-J. Bertin). Boston, MA: Birkhäuser, pp. 153-177, 1983.
Moore, R. and van der Poorten, A. "On the Thermodynamics of Curves and Other Curlicues." McQuarie Univ. Math. Rep. 89-0031, April 1989.
Pickover, C. A. Mazes for the Mind: Computers and the Unexpected. New York: St. Martin's Press, 1993.
Pickover, C. A. "Is the Fractal Golden Curlicue Cold?" Visual Comput. 11, 309-312, 1995a.
Pickover, C. A. "The Fractal Golden Curlicue is Cool." Ch. 21 in Keys to Infinity. New York: W. H. Freeman, pp. 163-167, 1995b.
Sedgewick, R. Algorithms in C, 3rd ed. Reading, MA: Addison-Wesley, 1998.
Stewart, I. Another Fine Math You've Got Me Into.... New York: W. H. Freeman, 1992.
Stoschek, E. "Module 35: Curlicue Variations: Polygon Patterns in the Gauss Plane of Complex Numbers." http://marvin.sn.schule.de/~inftreff/modul35/task35_e.htm.
Stoschek, E. "Module 36: The Feigenbaum-Constant 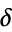 in the Gauss Plane." http://marvin.sn.schule.de/~inftreff/modul36/task36_e.htm.
in the Gauss Plane." http://marvin.sn.schule.de/~inftreff/modul36/task36_e.htm.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|